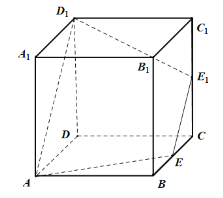
【題目】如圖，正方體
的棱長為2，
、
分別為棱
、
上的點，且與頂點不重合.
（1）若直線
與
相交于點
，求證：
、
、三點共線；
（2）若、分別為、的中點.
（ⅰ）求證：幾何體
為棱臺；
（ⅱ）求棱臺的體積.
（附：棱臺的體積公式
，其中
、
分別為棱臺上下底面積，
為棱臺的高）
【答案】（1）證明見解析；（2）（ⅰ）證明見解析；（ⅱ）
【解析】
（1）由
平面
，平面
，平面
平面
，根據點在兩個不重合的面內，則點在兩個面的公共線上即可證出.
（2）（ⅰ）連
，
、
分別為棱
、
的中點，證出四邊形
為梯形，從而可得
與
相交，再由（1）可得直線、
、交于一點，由平面
平面
，即可證出.
（ⅱ）求出
，
，以及棱臺的高
，代入棱臺的體積公式即可求解.
證明：（1）
，
，
，
平面，
平面，
平面，平面，
即點
為平面與平面的公共點.
又
平面平面，
，即
、
、三點共線.
（2）（ⅰ）連，
、分別為棱、的中點，
為
的中位線，
，
，
，
，
四邊形
為平行四邊形.
，
，
，
，
四邊形為梯形，
與相交.
由（1）知：直線、、交于一點，
又平面平面，
幾何體
為三棱臺.
（ⅱ）由題意：
，
，，
，
即棱臺的體積是.
第三學期贏在暑假系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案科目：高中數學 來源： 題型：
【題目】已知A，B，C分別為△ABC的三邊a，b，c所對的角，向量
＝(sin A，sin B)，
＝(cos B，cos A)，且
＝sin 2C.
(1)求角C的大小；
(2)若sin A，sin C，sin B成等差數列，且
，求邊c的長.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，三棱柱ABC﹣A1B1C1中，所有棱長均相等，且AA1⊥平面ABC，點D、E、F分別為所在棱的中點．
（1）求證：EF∥平面CDB1；
（2）求異面直線EF與BC所成角的余弦值；
（3）求二面角B1﹣CD﹣B的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(2017·衢州調研)已知四棱錐P－ABCD的底面ABCD是菱形，∠ADC＝120°，AD的中點M是頂點P在底面ABCD的射影，N是PC的中點.
(1)求證：平面MPB⊥平面PBC；
(2)若MP＝MC，求直線BN與平面PMC所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
