
【題目】已知函數f(x)![]() lg
lg![]() .
.
(1)判斷并證明函數f(x)的單調性;
(2)解關于x的不等式![]() .
.
【答案】(1)f(x)在(0,4)上單調遞減,見解析(2)(0,1)∪(2,3).
【解析】
(1)先求解定義域,再取區間內![]() ,再計算
,再計算![]() 的正負即可.
的正負即可.
(2)先求得![]() ,再根據函數的單調性將不等式轉換為
,再根據函數的單調性將不等式轉換為![]() 求解即可.
求解即可.
(1)f(x)的定義域為(0,4),
f(x)在(0,4)上單調遞減,證明如下:
設0<x1<x2<4,則:
![]() ,
,
∵0<x1<x2<4,
∴x2﹣x1>0,x1x2>0,4﹣x1>4﹣x2>0,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴f(x1)>f(x2),
∴f(x)在(0,4)上單調遞減;
(2)∵f(1)=1+lg3,
由![]() 得,
得,![]() ,
,
∵f(x)在(0,4)上單調遞減,
∴![]() ,解得0<x<1或2<x<3,
,解得0<x<1或2<x<3,
∴原不等式的解集為(0,1)∪(2,3).


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知定義域為R的函數f(x)=![]() 是奇函數.
是奇函數.
(1)求b的值,判斷并用定義法證明f(x)在R上的單調性;
(2)解不等式f(2x+1)+f(x)<0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)滿足f(x+1)-f(x)=-2x+1,且f(2)=15.
(1)求函數f(x)的解析式;
(2) 令g(x)=(2-2m)x-f(x).
① 若函數g(x)在x∈[0,2]上是單調函數,求實數m的取值范圍;
② 求函數g(x)在x∈[0,2]上的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
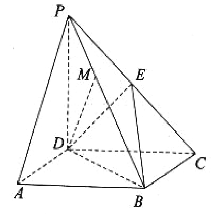
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一點.
上的一點.
(1)若![]() 平面
平面![]() ,證明:
,證明:![]() ;
;
(2)在(1)的條件下,棱![]() 上是否存在點
上是否存在點![]() ,使直線
,使直線![]() 與平面
與平面![]() 所成角的大小為
所成角的大小為![]() ?若存在,求
?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于![]() 的說法,正確的是( )
的說法,正確的是( )
A.展開式中的二項式系數之和為2048
B.展開式中只有第6項的二項式系數最大
C.展開式中第6項和第7項的二項式系數最大
D.展開式中第6項的系數最小
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義域為D的函數y=f(x),如果存在區間[m,n]![]() D,同時滿足:
D,同時滿足:
①f(x)在[m,n]內是單調函數;
②當定義域是[m,n]時,f(x)的值域也是[m,n].則稱[m,n]是該函數的“和諧區間”.
(1)證明:[0,1]是函數y=f(x)=x2的一個“和諧區間”.
(2)求證:函數![]() 不存在“和諧區間”.
不存在“和諧區間”.
(3)已知:函數![]() (a∈R,a≠0)有“和諧區間”[m,n],當a變化時,求出n﹣m的最大值.
(a∈R,a≠0)有“和諧區間”[m,n],當a變化時,求出n﹣m的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 為常數,函數
為常數,函數![]() .給出以下結論:
.給出以下結論:
①若![]() ,則
,則![]() 在區間
在區間![]() 上有唯一零點;
上有唯一零點;
②若![]() ,則存在實數
,則存在實數![]() ,當
,當![]() 時,
時,![]()
![]() ;
;
③若![]() ,則當
,則當![]() 時,
時,![]() .
.
其中正確結論的個數是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小李從網上購買了一件商品,快遞員計劃在下午5:00-6:00之間送貨上門,已知小李下班到家的時間為下午5:30-6:00.快遞員到小李家時,如果小李未到家,則快遞員會電話聯系小李.若小李能在10分鐘之內到家,則快遞員等小李回來;否則,就將商品存放在快遞柜中.則小李需要去快遞柜收取商品的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com