
分析 (1)求得不等式f(x)≤2的解集,再根據不等式f(x)≤2的解集為{x|-1≤x≤5},求得實數m的值.
(2)由題意可得g(x)=|x-2|+|x+3|的最小值大于或等于t-2,求得g(x)=|x-2|+|x+3|的最小值,可得t的范圍.
解答 解:(1)由f(x)≤2得,|x-m|≤3,解得m-3≤x≤m+3,
又已知不等式f(x)≤2的解集為{x|-1≤x≤5},∴$\left\{\begin{array}{l}m-3=-1\\ m+3=5\end{array}\right.$,解得m=2.
(2)當m=2時,f(x)=|x-2|-1,由于f(x)+f(x+5)≥t-2對一切實數x恒成立,
則|x-2|+|x+3|-2≥t-2對一切實數x恒成立,即|x-2|+|x+3|≥t對一切實數x恒成立,
設g(x)=|x-2|+|x+3|,
于是$g(x)=|x-2|+|x+3|=\left\{\begin{array}{l}-2x-1,x<-3\\ 5,-3≤x≤2\\ 2x+1,x>2.\end{array}\right.$,
所以當x<-3時,g(x)>5;當-3≤x≤2時,g(x)=5;當x>2時,g(x)>5.
綜上可得,g(x)的最小值為5,∴t≤5,
即t的取值范圍為(-∞,5].
點評 本題主要考查絕對值不等式的解法,函數的恒成立問題,體現了轉化的數學思想,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
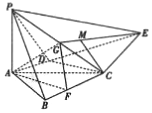 在四棱錐P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G為PC的中點,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分別為BC,EG上一點,且AF∥CD.
在四棱錐P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G為PC的中點,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分別為BC,EG上一點,且AF∥CD.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | an=n | B. | an=n2 | C. | an=$\frac{n}{2}$ | D. | an=$\frac{{n}^{2}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}-1$ | D. | $2-\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
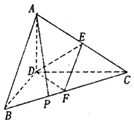 已知三棱錐A-BCD,AD⊥平面BCD,BD⊥CD,AD=BD=2,CD=2$\sqrt{3}$,E,F分別是AC,BC的中點.
已知三棱錐A-BCD,AD⊥平面BCD,BD⊥CD,AD=BD=2,CD=2$\sqrt{3}$,E,F分別是AC,BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
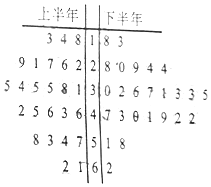 自貢某工廠于2016年下半年對生產工藝進行了改造(每半年為一個生產周期),從2016年一年的產品中用隨機抽樣的方法抽取了容量為50的樣本,用莖葉圖表示(如圖).已知每個生產周期內與其中位數誤差在±5范圍內(含±5)的產品為優質品,與中位數誤差在±15范圍內(含±15)的產品為合格品(不包括優質品),與中位數誤差超過±15的產品為次品.企業生產一件優質品可獲利潤20元,生產一件合格品可獲利潤10元,生產一件次品要虧損10元
自貢某工廠于2016年下半年對生產工藝進行了改造(每半年為一個生產周期),從2016年一年的產品中用隨機抽樣的方法抽取了容量為50的樣本,用莖葉圖表示(如圖).已知每個生產周期內與其中位數誤差在±5范圍內(含±5)的產品為優質品,與中位數誤差在±15范圍內(含±15)的產品為合格品(不包括優質品),與中位數誤差超過±15的產品為次品.企業生產一件優質品可獲利潤20元,生產一件合格品可獲利潤10元,生產一件次品要虧損10元| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com