
【題目】某企業生產 ![]() ,
, ![]() 兩種產品,根據市場調查與預測,
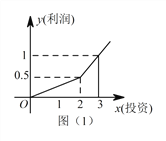
兩種產品,根據市場調查與預測, ![]() 產品的利潤與投資關系如圖(1)所示;
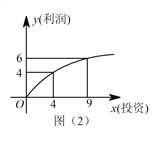
產品的利潤與投資關系如圖(1)所示; ![]() 產品的利潤與投資的算術平方根成正比,其關系如圖(2)所示(注:利潤和投資單位:萬元).
產品的利潤與投資的算術平方根成正比,其關系如圖(2)所示(注:利潤和投資單位:萬元).
(1)分別將 ![]() ,
, ![]() 兩種產品的利潤表示為投資的函數關系式;
兩種產品的利潤表示為投資的函數關系式;
(2)已知該企業已籌集到 ![]() 萬元資金,并將全部投入
萬元資金,并將全部投入 ![]() ,
, ![]() 兩種產品的生產.問怎樣分配這
兩種產品的生產.問怎樣分配這 ![]() 萬元投資,才能使該企業獲得最大利潤?其最大利潤約為多少萬元?
萬元投資,才能使該企業獲得最大利潤?其最大利潤約為多少萬元?
【答案】(1)![]() ;(2)投入
;(2)投入 ![]() 產品
產品 ![]() 萬元,
萬元, ![]() 產品
產品 ![]() 萬元時,總利潤最大值為
萬元時,總利潤最大值為 ![]() 萬元
萬元
【解析】試題分析:(1)對于A,當0≤x≤2時,因為圖象過(2,0.5)和原點,當x>2時,圖象過(2,0.5)和(3,1),可得函數的解析式;對于B,易知y=2![]() (x≥0).
(x≥0).
(2)設投入B產品x萬元,則投入A產品(18-x)萬元,利潤為y萬元.分16≤x≤18時,0≤x<16時兩種情況求出函數的最大值,比較后可得答案.
試題解析:
(1) 對于 ![]() ,當
,當 ![]() 時,因為圖象過
時,因為圖象過 ![]() ,所以
,所以 ![]() ,
,
當 ![]() 時,令
時,令 ![]() ,因圖象過
,因圖象過 ![]() 和
和 ![]() ,得
,得 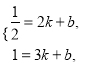
解得 ![]() ,
, ![]() ,故
,故 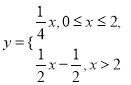
對于 ![]() ,易知
,易知 ![]() .
.
(2) 設投入 ![]() 產品
產品 ![]() 萬元,則投入
萬元,則投入 ![]() 產品
產品 ![]() 萬元,利潤為
萬元,利潤為 ![]() 萬元.
萬元.
若 ![]() 時,則
時,則 ![]() ,則投入
,則投入 ![]() 產品的利潤為
產品的利潤為 ![]() ,投入
,投入 ![]() 產品的利潤為
產品的利潤為 ![]() ,則
,則 ![]() ,令
,令 ![]() ,
, ![]() ,
,
則 ![]() ,此時當
,此時當 ![]() ,即
,即 ![]() 時,
時, ![]() 萬元;
萬元;
當 ![]() 時,
時, ![]() ,則投入
,則投入 ![]() 產品的利潤為
產品的利潤為 ![]() ,投入
,投入 ![]() 產品的利潤為
產品的利潤為 ![]() ,則
,則 ![]() ,令
,令 ![]() ,
, ![]() ,
,
則 ![]() ,當
,當 ![]() 時,即
時,即 ![]() 時,
時, ![]() 萬元;
萬元;
由 ![]() ,
,
綜上,投入 ![]() 產品
產品 ![]() 萬元,
萬元, ![]() 產品
產品 ![]() 萬元時,總利潤最大值為
萬元時,總利潤最大值為 ![]() 萬元.
萬元.


科目:高中數學 來源: 題型:
【題目】學校藝術節對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,我海監船在![]() 島海域例行維權巡航,某時刻航行至
島海域例行維權巡航,某時刻航行至![]() 處,此時測得其東北方向與它相距
處,此時測得其東北方向與它相距![]() 海里的
海里的![]() 處有一外國船只,且
處有一外國船只,且![]() 島位于海監船正東
島位于海監船正東![]() 海里處.
海里處.
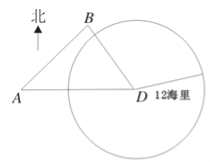
(1)求此時該外國船只與![]() 島的距離;
島的距離;
(2)觀測中發現,此外國船只正以每小時![]() 海里的速度沿正南方向航行,為了將該船攔截在離
海里的速度沿正南方向航行,為了將該船攔截在離![]() 島
島![]() 海里處,不讓其進入
海里處,不讓其進入![]() 島
島![]() 海里內的海域,試確定海監船的航向,并求其速度的最小值.(參考數據:
海里內的海域,試確定海監船的航向,并求其速度的最小值.(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,與
兩點,與![]() 軸,
軸, ![]() 軸分別相交于點
軸分別相交于點![]() 和點
和點![]() ,且
,且![]() ,點
,點![]() 是點
是點![]() 關于
關于![]() 軸的對稱點,
軸的對稱點, ![]() 的延長線交橢圓于點
的延長線交橢圓于點![]() ,過點
,過點![]() 分別做
分別做![]() 軸的垂線,垂足分別為
軸的垂線,垂足分別為![]() .
.
(1) 若橢圓![]() 的左、右焦點與其短軸的一個端點是正三角形的三個頂點,點
的左、右焦點與其短軸的一個端點是正三角形的三個頂點,點![]() 在橢圓
在橢圓![]() 上,求橢圓
上,求橢圓![]() 的方程;
的方程;
(2)當![]() 時,若點
時,若點![]() 平分線段
平分線段![]() ,求橢圓
,求橢圓![]() 的離心率.
的離心率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的長軸長為
的長軸長為![]() ,
, ![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程和離心率.
的方程和離心率.
(2)設點![]() ,動點
,動點![]() 在
在![]() 軸上,動點
軸上,動點![]() 在橢圓
在橢圓![]() 上,且點
上,且點![]() 在
在![]() 軸的右側.若
軸的右側.若![]() ,求四邊形
,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某土特產銷售總公司為了解其經營狀況,調查了其下屬各分公司月銷售額和利潤,得到數據如下表:
分公司名稱 | 雅雨 | 雅魚 | 雅女 | 雅竹 | 雅茶 |
月銷售額 | 3 | 5 | 6 | 7 | 9 |
月利潤額 | 2 | 3 | 3 | 4 | 5 |
在統計中發現月銷售額![]() 和月利潤額
和月利潤額![]() 具有線性相關關系.
具有線性相關關系.
(1)根據如下的參考公式與參考數據,求月利潤額![]() 與月銷售額
與月銷售額![]() 之間的線性回歸方程;
之間的線性回歸方程;
(2)若該總公司還有一個分公司“雅果”月銷售額為10萬元,試估計它的月利潤額是多少?
(參考公式: 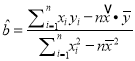 ,
, ![]() ,其中:
,其中: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的離心率為
)的離心率為![]() ,以橢圓的四個頂點為頂點的四邊形的面積為8.
,以橢圓的四個頂點為頂點的四邊形的面積為8.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)如圖,斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,點
兩點,點![]() 在直線
在直線![]() 的左上方.若
的左上方.若![]() ,且直線
,且直線![]() ,
, ![]() 分別與
分別與![]() 軸交于
軸交于![]() ,
, ![]() 點,求線段
點,求線段![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是橢圓
是橢圓![]() 的左、右焦點,
的左、右焦點, ![]() 為坐標原點,點
為坐標原點,點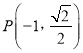 在橢圓上,線段
在橢圓上,線段![]() 與
與![]() 軸的交點
軸的交點![]() 滿足
滿足![]() .
.
(Ⅰ)求橢圓的標準方程;
(Ⅱ)圓![]() 是以
是以![]() 為直徑的圓,一直線
為直徑的圓,一直線![]() 與圓
與圓![]() 相切,并與橢圓交于不同的兩點
相切,并與橢圓交于不同的兩點![]() 、
、![]() ,當
,當![]() ,且滿足
,且滿足![]() 時,求
時,求![]() 的面積
的面積![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com