
【題目】(重點班)我們知道對數函數![]() ,對任意
,對任意![]() ,都有
,都有![]() 成立,若
成立,若![]() ,則當
,則當![]() 時,
時,![]() .參照對數函數的性質,研究下題:定義在
.參照對數函數的性質,研究下題:定義在![]() 上的函數
上的函數![]() 對任意
對任意![]() ,都有
,都有![]() ,并且當且僅當
,并且當且僅當![]() 時,
時,![]() 成立.
成立.
(1)設![]() ,求證:
,求證:![]() ;
;
(2)設![]() ,若
,若![]() ,比較
,比較![]() 與
與![]() 的大小.
的大小.
科目:高中數學 來源: 題型:
【題目】如圖,把兩個全等的![]() 和
和![]() 分別置于平面直角坐標系中,使直角邊
分別置于平面直角坐標系中,使直角邊![]() 在
在![]() 軸上,已知點
軸上,已知點![]() ,過
,過![]() 兩點的直線分別交
兩點的直線分別交![]() 軸、
軸、![]() 軸于點
軸于點![]() . 拋物線
. 拋物線![]() 經過
經過![]() 三點.
三點.
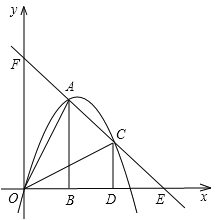
(1)求該拋物線的函數解析式;
(2)點![]() 為線段
為線段![]() 上的一個動點,過點
上的一個動點,過點![]() 作
作![]() 軸的平行線交拋物線于點
軸的平行線交拋物線于點![]() ,交
,交![]() 軸于點
軸于點![]() ,問是否存在這樣的點
,問是否存在這樣的點![]() ,使得四邊形
,使得四邊形![]() 為等腰梯形?若存在,求出此時點
為等腰梯形?若存在,求出此時點![]() 的坐標;若不存在,請說明理由;
的坐標;若不存在,請說明理由;
(3)若![]() 沿
沿![]() 方向平移(點
方向平移(點![]() 始終在線段
始終在線段![]() 上,且不與點
上,且不與點![]() 重合),
重合),![]() 在平移的過程中與
在平移的過程中與![]() 重疊部分的面積記為
重疊部分的面積記為![]() ,試探究
,試探究![]() 是否存在最大值?若存在,求出這個最大值;若不存在,請說明理由.
是否存在最大值?若存在,求出這個最大值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的質量以其指標值來衡量,其指標值越大表明質量越好,且指標值大于或等于102的產品為優質品.現用兩種新配方(分別稱為![]() 配方和
配方和![]() 配方)做試驗,各生產了100件這種產品,并測量了每件產品的指標值,得到了下面的試驗結果:
配方)做試驗,各生產了100件這種產品,并測量了每件產品的指標值,得到了下面的試驗結果:
![]() 配方的頻數分布表
配方的頻數分布表
指標值分組 |
|
|
|
|
|
頻數 | 8 | 20 | 42 | 22 | 8 |
![]() 配方的頻數分布表
配方的頻數分布表
指標值分組 |
|
|
|
|
|
頻數 | 4 | 12 | 42 | 32 | 10 |
(Ⅰ)分別估計用![]() 配方,
配方,![]() 配方生產的產品的優質品率;
配方生產的產品的優質品率;
(Ⅱ)已知用![]() 配方生產的一件產品的利潤
配方生產的一件產品的利潤![]() (單位:元)與其指標值
(單位:元)與其指標值![]() 的關系式為
的關系式為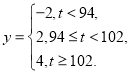
估計用![]() 配方生產的一件產品的利潤大于0的概率,并求用
配方生產的一件產品的利潤大于0的概率,并求用![]() 配方生產的上述產品平均每件的利潤。
配方生產的上述產品平均每件的利潤。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 截以原點
截以原點![]() 為圓心的圓所得的弦長為
為圓心的圓所得的弦長為![]() 。
。
(1)求圓![]() 的方程;
的方程;
(2)若直線![]() 與圓
與圓![]() 切于第一象限,且與坐標軸交于點
切于第一象限,且與坐標軸交于點![]() ,當
,當![]() 長最小時,求直線
長最小時,求直線![]() 的方程;
的方程;
(3)設![]() 是圓
是圓![]() 上任意兩點,點
上任意兩點,點![]() 關于
關于![]() 軸的對稱點
軸的對稱點![]() ,若直線
,若直線![]() 分別交
分別交![]() 軸于點
軸于點![]() 和
和![]() ,問
,問![]() 是否為定值?若是,請求出該定值;若不是,請說明理由。
是否為定值?若是,請求出該定值;若不是,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】堯盛機械生產廠每生產某產品![]() (百臺),其總成本為
(百臺),其總成本為![]() (萬元),其中固定成本為
(萬元),其中固定成本為![]() 萬元,并且每生產1百臺的生產成本為1萬元(總成本=固定成本+生產成本).銷售收入
萬元,并且每生產1百臺的生產成本為1萬元(總成本=固定成本+生產成本).銷售收入![]() (萬元)滿足
(萬元)滿足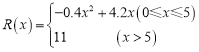 ,假定生產的產品都能賣掉,請完成下列問題:
,假定生產的產品都能賣掉,請完成下列問題:
(1)寫出利潤函數![]() 的解析式(注:利潤=銷售收入-總成本);
的解析式(注:利潤=銷售收入-總成本);
(2)試問該工廠生產多少臺產品時,可使盈利最多?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】調查200名50歲以上有吸煙習慣與患慢性氣管炎的人的情況,獲數據如下
患慢性氣管炎 | 未患慢性氣管炎 | 總計 | |
吸煙 |
| 30 | 100 |
不吸煙 | 35 |
| 100 |
合計 | 105 | 95 | 200 |
(1)表中![]() ,
,![]() 的值分別是多少;
的值分別是多少;
(2)試問:有吸煙習慣與患慢性氣管炎病是否有關?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某鎮計劃建造一個室內面積為800m2的矩形蔬菜溫室,在溫室內,沿左、右兩側與后側內墻各保留1m寬的通道,沿前側內墻保留3m寬的空地.當矩形溫室的邊長各為多少時,蔬菜的種植面積最大?最大種植面積是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com