【題目】已知f（x）=2sin4x+2cos4x+cos22x﹣3．
（1）求函數f（x）的最小正周期．
（2）求函數f（x）在閉區間[ 
]上的最小值并求當f（x）取最小值時，x的取值集合．
【答案】
（1）解：f（x）=2（sin2x+cos2x）2﹣4sin2xcos2x+cos22x﹣3
=2×1﹣sin22x+cos22x﹣3
=cos22x﹣sin22x﹣1
=cos4x﹣1
函數的最小正周期T= 
= 
（2）解：x∈[ 
]
4x∈[ 
]
∴f（x）=cos4x﹣1在[ ]是減函數
當x= 
時
f（x）有最小值f（ ）=cos 
﹣1=﹣ 
﹣1，此時x的集合是 
【解析】通過同角三角函數的基本關系式，二倍角公式化簡函數為一個角的一個三角函數的形式，（1）利用周期公式求出函數的最小正周期．（2）通過x∈[ ]，求出 4x∈[ ]，利用函數的單調性，求出函數的最小值，以及x的集合即可．
【考點精析】認真審題，首先需要了解二倍角的余弦公式(二倍角的余弦公式：
)．
捷徑訓練檢測卷系列答案
小夫子全能檢測系列答案科目：高中數學 來源： 題型：
【題目】已知圓x2+y2=4上一定點A（2，0），B（1，1）為圓內一點，P，Q為圓上的動點．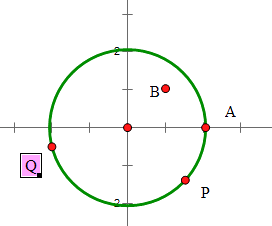 
（1）求線段AP中點的軌跡方程；
（2）若∠PBQ=90°，求線段PQ中點的軌跡方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an} 的前n項和Sn=3n2+8n，{bn}是等差數列，且an=bn+bn+1
（1）求數列{bn}的通項公式；
（2）令cn= 
，求數列{cn}的前n項和Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）是定義在R上的奇函數，當x≥0時f（x）=2x﹣x2 ，
（1）求f（x）的表達式；
（2）設0＜a＜b，當x∈[a，b]時，f（x）的值域為 
，求a，b的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
