某數列既成等差數列也成等比數列,那么該數列一定是( )
A.公差為0的等差數列
B.公比為1的等比數列
C.常數數列1,1,1
D.以上都不對
【答案】
分析:先設該數列的公比為q,公差為d,則q和d均為常數,進而通過a
n+1-a
n=d化簡得a
n(1-q)=d,討論當q≠1時a
n=
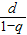
可推知數列{a
n}為常數列,與q≠1矛盾.進而推斷q=1.答案可知.
解答:解:設該數列為{a
n}公比為q,公差為d,則q和d均為常數,
則a
n+1-a
n=a
nq-a
n=a
n(1-q)=d
如果q≠1,則a
n=
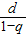
,為常數列,與q≠1矛盾.
故q必須等于1.
故選B
點評:本題主要考查了等比和等差數列性質的應用.屬基礎題.
