
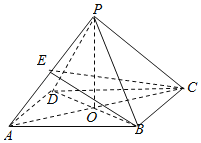
【題目】在四棱錐P﹣ABCD中,底面是邊長為2的菱形,∠BAD=60°,PB=PD=2,PA![]() ,AC∩BD=O
,AC∩BD=O

(1)設平面ABP∩平面DCP=l,證明:l∥AB
(2)若E是PA的中點,求三棱錐P﹣BCE的體積VP﹣BCE.
【答案】(1)見解析(2)![]()
【解析】
(1)根據(jù)線面平行的判定定理、性質(zhì)定理進行證明即可;
(2)根據(jù)菱形的性質(zhì)、等腰三角形的性質(zhì),線面垂直的判定定理可以證明出BD⊥面PAC,因此可以得到BO是三棱錐B﹣PCE的高.再結(jié)合等邊三角形的性質(zhì),結(jié)合勾股定理,三棱錐的體積公式進行求解即可.
證明:(1)因為AB∥DC,AB平面PDC,DC平面PDC,
所以AB∥平面PDC.
又平面ABP∩平面DCP=l,且AB面ABP,
所以l∥AB.
解:(2)因為底面是菱形,所以BD⊥AC.
因為PB=PD,且O是BD中點,所以BD⊥PO.
又PO∩AC=O,所以BD⊥面PAC.
所以BO是三棱錐B﹣PCE的高.
因為AO為邊長為2的等邊△ABD的中線,所以AO![]() .
.
因為PO為邊長為2的等邊△PBD的中線,所以PO![]() .
.
在△POA中,PA![]() ,AO
,AO![]() ,PO
,PO![]() ,
,
所以AO2+PO2=PA2,所以PO⊥AO.
所以![]() ,
,
因為E是線段PA的中點,所以![]() .
.
所以三棱錐P﹣BCE 的體積:
VP﹣BCE=VB﹣PCE![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】為了調(diào)查居民對城市共享單車的滿意度,隨機選取了100人進行問卷調(diào)查,并將問卷中的100人根據(jù)其滿意度評分值按照![]() 分為5組,得到號如圖所示的頻率分布直方圖.
分為5組,得到號如圖所示的頻率分布直方圖.
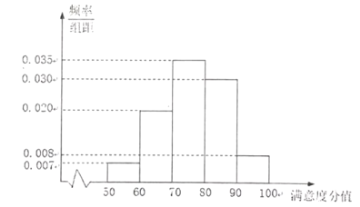
(Ⅰ)求滿意度分值不低于70分的人數(shù).
(Ⅱ)已知滿意度分值在![]() 內(nèi)的男性與女性的比為3:4,為提高共享單車的滿意度,現(xiàn)從滿意度分值在
內(nèi)的男性與女性的比為3:4,為提高共享單車的滿意度,現(xiàn)從滿意度分值在![]() 的人中隨機抽取2人進行座談,求這2人中只有一位男性的概率.
的人中隨機抽取2人進行座談,求這2人中只有一位男性的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某工廠甲、乙、丙三個車間生產(chǎn)了同一種產(chǎn)品,數(shù)量分別為120件,60件,30件.為了解它們的產(chǎn)品質(zhì)量是否存在顯著差異,用分層抽樣方法抽取了一個容量為n的樣本進行調(diào)查,其中從乙車間的產(chǎn)品中抽取了2件。
(Ⅰ)應從甲、丙兩個車間的產(chǎn)品中分別抽取多少件,樣本容量n為多少?
(Ⅱ)設抽出的n件產(chǎn)品分別用![]() ,
,![]() ,…,
,…,![]() 表示,現(xiàn)從中隨機抽取2件產(chǎn)品。
表示,現(xiàn)從中隨機抽取2件產(chǎn)品。
(i)試用所給字母列舉出所有可能的抽取結(jié)果;
(ii)設M為事件“抽取的2件產(chǎn)品來自不同車間”,求事件M發(fā)生的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求![]() 的極值;
的極值;
(2)證明:![]() 時,
時,![]()
(3)若函數(shù)![]() 有且只有三個不同的零點,分別記為
有且只有三個不同的零點,分別記為![]() ,設
,設![]() 且
且![]() 的最大值是
的最大值是![]() ,證明:
,證明:![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】坐標系與參數(shù)方程:在平面直角坐標系中,以原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,已知點
軸的非負半軸為極軸建立極坐標系,已知點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() ,且點
,且點![]() 在直線
在直線![]() 上
上
(Ⅰ)求![]() 的值和直線
的值和直線![]() 的直角坐標方程及
的直角坐標方程及![]() 的參數(shù)方程;
的參數(shù)方程;
(Ⅱ)已知曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() ,(
,(![]() 為參數(shù)),直線
為參數(shù)),直線![]() 與
與![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值
的值
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】![]() 是指大氣中直徑小于或等于
是指大氣中直徑小于或等于![]() 微米的顆粒物,也稱為可入肺顆粒物.雖然
微米的顆粒物,也稱為可入肺顆粒物.雖然![]() 只是地球大氣成分中含量很少的組分,但它對空氣質(zhì)量和能見度等有重要的影響.我國
只是地球大氣成分中含量很少的組分,但它對空氣質(zhì)量和能見度等有重要的影響.我國![]() 標準如下表所示.我市環(huán)保局從市區(qū)四個監(jiān)測點2018年全年每天的
標準如下表所示.我市環(huán)保局從市區(qū)四個監(jiān)測點2018年全年每天的![]() 監(jiān)測數(shù)據(jù)中隨機抽取
監(jiān)測數(shù)據(jù)中隨機抽取![]() 天的數(shù)據(jù)作為樣本,監(jiān)測值如莖葉圖如圖所示.
天的數(shù)據(jù)作為樣本,監(jiān)測值如莖葉圖如圖所示.
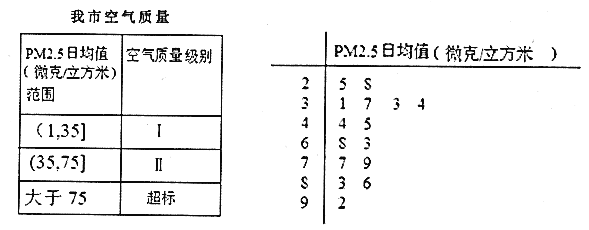
(Ⅰ)求這![]() 天數(shù)據(jù)的平均值;
天數(shù)據(jù)的平均值;
(Ⅱ)從這![]() 天的數(shù)據(jù)中任取
天的數(shù)據(jù)中任取![]() 天的數(shù)據(jù),記表示其中空氣質(zhì)量達到一級的天數(shù)
天的數(shù)據(jù),記表示其中空氣質(zhì)量達到一級的天數(shù)![]() ,求
,求![]() 的分布列和數(shù)學期望;
的分布列和數(shù)學期望;
(Ⅲ)以![]() 天的
天的![]() 日均值來估計一年的空氣質(zhì)量情況,則一年(按
日均值來估計一年的空氣質(zhì)量情況,則一年(按![]() 天計算)中大約有多少天的空氣質(zhì)量達到一級.
天計算)中大約有多少天的空氣質(zhì)量達到一級.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 在
在![]() 上單調(diào)遞減,求
上單調(diào)遞減,求![]() 的取值范圍;
的取值范圍;
(2)若![]() 在
在![]() 處取得極值,判斷當
處取得極值,判斷當![]() 時,存在幾條切線與直線
時,存在幾條切線與直線![]() 平行,請說明理由;
平行,請說明理由;
(3)若![]() 有兩個極值點
有兩個極值點![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】甲、乙兩超市同時開業(yè),第一年的全年銷售額為a萬元,由于經(jīng)營方式不同,甲超市前n年的總銷售額為![]() (n2-n+2)萬元,乙超市第n年的銷售額比前一年銷售額多a
(n2-n+2)萬元,乙超市第n年的銷售額比前一年銷售額多a![]() 萬元.
萬元.
(1)求甲、乙兩超市第n年銷售額的表達式;
(2)若其中某一超市的年銷售額不足另一超市的年銷售額的50%,則該超市將被另一超市收購,判斷哪一超市有可能被收購?如果有這種情況,將會出現(xiàn)在第幾年?
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com