【題目】某旅游區每年各個月份接待游客的人數近似地滿足周期性規律，因而第
個月從事旅游服務工作的人數
可近似地用函數
來刻畫，其中正整數表示月份且
，例如
表示1月份，
和
是正整數，
，
. 統計發現，該地區每年各個月份從事旅游服務工作的人數有以下規律：
① 每年相同的月份，該地區從事旅游服務工作的人數基本相同；
② 該地區從事旅游服務工作的人數最多的8月份和最少的2月份相差400人；
③ 2月份該地區從事旅游服務工作的人數為100人，隨后逐月遞增直到8月份達到最多.
（1）試根據已知信息，求的表達式；
（2）一般地，當該地區從事旅游服務工作的人數在400或400以上時，該地區也進入了一年中的旅游“旺季”，那么，一年中的哪幾個月是該地區的旅游“旺季”？請說明理由.
科目：高中數學 來源： 題型：
【題目】某老小區建成時間較早，沒有集中供暖，隨著人們生活水平的日益提高熱力公司決定在此小區加裝暖氣該小區的物業公司統計了近五年（截止2018年年底）小區居民有意向加裝暖氣的戶數，得到如下數據
年份編號x | 1 | 2 | 3 | 4 | 5 |
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
加裝戶數y | 34 | 95 | 124 | 181 | 216 |
（Ⅰ）若有意向加裝暖氣的戶數y與年份編號x滿足線性相關關系求y與x的線性回歸方程并預測截至2019年年底，該小區有多少戶居民有意向加裝暖氣；
（Ⅱ）2018年年底鄭州市民生工程決定對老舊小區加裝暖氣進行補貼，該小區分到120個名額物業公司決定在2019年度采用網絡競拍的方式分配名額，競拍方案如下：①截至2018年年底已登記在冊的居民擁有競拍資格；②每戶至多申請一個名額，由戶主在競拍網站上提出申請并給出每平方米的心理期望報價；③根據物價部門的規定，每平方米的初裝價格不得超過300元；④申請階段截止后，將所有申請居民的報價自高到低排列，排在前120位的業主以其報價成交；⑤若最后出現并列的報價，則認為申請時問在前的居民得到名額，為預測本次競拍的成交最低價，物業公司隨機抽取了有競拍資格的50位居民進行調查統計了他們的擬報競價，得到如圖所示的頻率分布直方圖：
（1）求所抽取的居民中擬報競價不低于成本價180元的人數；
（2）如果所有符合條件的居民均參與競拍，請你利用樣本估計總體的思想預測至少需要報價多少元才能獲得名額（結果取整數）
參考公式對于一組數據（x1，y1），（x2，y2），（x3，y3），…（xn，yn），其回歸直線
的斜率和截距的最小二乘估計分別為，
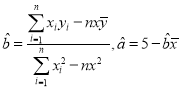
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某玩具廠生產出一種新型兒童泡沫玩具飛機,為更精確的確定最終售價,該廠采用了多種價格對該玩具飛機進行了試銷,某銷售點的銷售情況如下表:
單價 | 8 | 9 | 10 | 11 | 12 |
銷量 | 40 | 36 | 30 | 24 | 20 |
從散點圖可以看出,這些點大致分布在一條直線的附近,變量
,
有較強的線性相關性.
(1)求銷量關于的回歸方程;
(2)若每架該玩具飛機的成本價為5元,利用(1)的結果,預測每架該玩具飛機的定價為多少元時,總利潤最大.(結果保留一位小數)
(附:
,
,
,
.)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】材料一：2018年，全國逾半省份將從秋季入學的高一年級開始實行新的學業水平考試和高考制度．所有省級行政區域均突破文理界限，由學生跨文理選科，均設 置“
”的考試科目．前一個“3”為必考科目，為統一高考科目語文、數學、外語.除個別省級行政區域仍執行教育部委托的分省命題任務外，絕大部分省級行政區域均由教育部考試中心統一命題；后一個“3”為高中學業水平考試（簡稱“學考”）選考科目，由各省級行政區域自主命題．材料二：2019年4月，河北、遼寧、江蘇、福建、湖北、湖南、廣東、重慶等8省市發布高考綜合改革實施方案，方案決定從2018年秋季入學的高中一年級學生開始實施高考綜合改革．考生總成績由全國統一高考的語文、數學、外語3個科目成績和考生選擇的3科普通高中學業水平選擇性考試科目成績組成，滿分為750分．即通常所說的“
”模式，所謂“”，即“3”是三門主科，分別是語文、數學、外語，這三門科目是必選的．“1”指的是要在物理、歷史里選一門，按原始分計入成績．“2”指考生要在生物、化學、思想政治、地理4門中選擇2門．但是這幾門科目不以原始分計入成績，而是等級賦分．等級賦分指的是把考生的原始成績根據人數的比例分為
、
、
、
、
五個等級，五個等級分別對應著相應的分數區間，然后再用公式換算，轉換得出分數．
（1）若按照“”模式選科，求選出的六科中含有“語文，數學，外語，物理，化學”的概率．
（2）某教育部門為了調查學生語數外三科成績與選科之間的關系，現從當地不同層次的學校中抽取高一學生2500名參加語數外的網絡測試，滿分450分，并給前400名頒發榮譽證書，假設該次網絡測試成績服從正態分布，且滿分為450分；
①考生甲得知他的成績為270分，考試后不久了解到如下情況：“此次測試平均成績為171分，351分以上共有57人”，問甲能否獲得榮譽證書，請說明理由；
②考生丙得知他的實際成績為430分，而考生乙告訴考生丙：“這次測試平均成績為201分，351分以上共有57人”，請結合統計學知識幫助丙同學辨別乙同學 信息的真偽．
附：
；
；
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某客戶準備在家中安裝一套凈水系統，該系統為三級過濾，使用壽命為十年.如圖所示，兩個一級過濾器采用并聯安裝，二級過濾器與三級過濾器為串聯安裝。
其中每一級過濾都由核心部件濾芯來實現。在使用過程中，一級濾芯和二級濾芯都需要不定期更換（每個濾芯是否需要更換相互獨立），三級濾芯無需更換，若客戶在安裝凈水系統的同時購買濾芯，則一級濾芯每個
元，二級濾芯每個
元.若客戶在使用過程中單獨購買濾芯，則一級濾芯每個
元，二級濾芯每個
元。現需決策安裝凈水系統的同時購濾芯的數量，為此參考了根據
套該款凈水系統在十年使用期內更換濾芯的相關數據制成的圖表，其中圖是根據個一級過濾器更換的濾芯個數制成的柱狀圖，表是根據個二級過濾器更換的濾芯個數制成的頻數分布表.
二級濾芯更換頻數分布表
二級濾芯更換的個數 |
|
|
頻數 |
|
|
以個一級過濾器更換濾芯的頻率代替
個一級過濾器更換濾芯發生的概率，以個二級過濾器更換濾芯的頻率代替個二級過濾器更換濾芯發生的概率.
（1）求一套凈水系統在使用期內需要更換的各級濾芯總個數恰好為
的概率；
（2）記
表示該客戶的凈水系統在使用期內需要更換的一級濾芯總數，求的分布列及數學期望；
（3）記
，
分別表示該客戶在安裝凈水系統的同時購買的一級濾芯和二級濾芯的個數.若
，且
，以該客戶的凈水系統在使用期內購買各級濾芯所需總費用的期望值為決策依據，試確定，的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓
的離心率為
，以橢圓四個頂點為頂點的四邊形的面積為
.
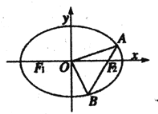
（1）求橢圓E的方程；
（2）過橢圓E的右焦點
作直線
與E交于A，B兩點，O為坐標原點，求
面積的最大值，并求此時直線的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
