
【題目】某客戶準備在家中安裝一套凈水系統,該系統為三級過濾,使用壽命為十年.如圖所示,兩個一級過濾器采用并聯安裝,二級過濾器與三級過濾器為串聯安裝。

其中每一級過濾都由核心部件濾芯來實現。在使用過程中,一級濾芯和二級濾芯都需要不定期更換(每個濾芯是否需要更換相互獨立),三級濾芯無需更換,若客戶在安裝凈水系統的同時購買濾芯,則一級濾芯每個![]() 元,二級濾芯每個
元,二級濾芯每個![]() 元.若客戶在使用過程中單獨購買濾芯,則一級濾芯每個
元.若客戶在使用過程中單獨購買濾芯,則一級濾芯每個![]() 元,二級濾芯每個
元,二級濾芯每個![]() 元。現需決策安裝凈水系統的同時購濾芯的數量,為此參考了根據
元。現需決策安裝凈水系統的同時購濾芯的數量,為此參考了根據![]() 套該款凈水系統在十年使用期內更換濾芯的相關數據制成的圖表,其中圖是根據
套該款凈水系統在十年使用期內更換濾芯的相關數據制成的圖表,其中圖是根據![]() 個一級過濾器更換的濾芯個數制成的柱狀圖,表是根據
個一級過濾器更換的濾芯個數制成的柱狀圖,表是根據![]() 個二級過濾器更換的濾芯個數制成的頻數分布表.
個二級過濾器更換的濾芯個數制成的頻數分布表.

二級濾芯更換頻數分布表
二級濾芯更換的個數 |
|
|
頻數 |
|
|
以![]() 個一級過濾器更換濾芯的頻率代替
個一級過濾器更換濾芯的頻率代替![]() 個一級過濾器更換濾芯發生的概率,以
個一級過濾器更換濾芯發生的概率,以![]() 個二級過濾器更換濾芯的頻率代替
個二級過濾器更換濾芯的頻率代替![]() 個二級過濾器更換濾芯發生的概率.
個二級過濾器更換濾芯發生的概率.
(1)求一套凈水系統在使用期內需要更換的各級濾芯總個數恰好為![]() 的概率;
的概率;
(2)記![]() 表示該客戶的凈水系統在使用期內需要更換的一級濾芯總數,求
表示該客戶的凈水系統在使用期內需要更換的一級濾芯總數,求![]() 的分布列及數學期望;
的分布列及數學期望;
(3)記![]() ,
,![]() 分別表示該客戶在安裝凈水系統的同時購買的一級濾芯和二級濾芯的個數.若
分別表示該客戶在安裝凈水系統的同時購買的一級濾芯和二級濾芯的個數.若![]() ,且
,且![]() ,以該客戶的凈水系統在使用期內購買各級濾芯所需總費用的期望值為決策依據,試確定
,以該客戶的凈水系統在使用期內購買各級濾芯所需總費用的期望值為決策依據,試確定![]() ,
,![]() 的值.
的值.
【答案】(1)![]() ;(2)見解析;(3)
;(2)見解析;(3)![]() =23,
=23,![]() =5.
=5.
【解析】
(1)根據圖表,若一套凈水系統在使用期內需要更換的各級濾芯總個數恰好為![]() ,則一級
,則一級![]() 個濾芯,二級
個濾芯,二級![]() 個濾芯,分別算出相應的概率,一次更換為2個一級濾芯和1個二級濾芯,從而得到概率.
個濾芯,分別算出相應的概率,一次更換為2個一級濾芯和1個二級濾芯,從而得到概率.
(2)由柱狀圖,一級過濾器需要更換的濾芯個數,分別得到概率,然后得到![]() 可能取的值,算出每種情況的概率,寫出分布列及數學期望.
可能取的值,算出每種情況的概率,寫出分布列及數學期望.
(3)因為![]() 且
且![]() ,則可分為兩類,即
,則可分為兩類,即![]() 和
和![]() ,分別計算他們的數學期望,然后進行比較,選取較小的一組.
,分別計算他們的數學期望,然后進行比較,選取較小的一組.
(1)由題意可知,若一套凈水系統在使用期內需要更換的各級濾芯總個數恰好為![]() ,則該套凈水系統中的兩個一級過濾器均需更換
,則該套凈水系統中的兩個一級過濾器均需更換![]() 個濾芯,二級過濾器需要更換
個濾芯,二級過濾器需要更換![]() 個濾芯。設“一套凈水系統在使用期內需要更換的各級濾芯總個數恰好為
個濾芯。設“一套凈水系統在使用期內需要更換的各級濾芯總個數恰好為![]() ”為事件
”為事件![]() .
.
因為一個一級過濾器需要更換![]() 個濾芯的概率為
個濾芯的概率為![]() ,二級過濾器需要更換
,二級過濾器需要更換![]() 個濾芯的概率為
個濾芯的概率為![]() ,
,
所以![]() .
.
(2)由柱狀圖可知,
一個一級過濾器需要更換的濾芯個數為![]() ,
,![]() ,
,![]() 的概率分別為
的概率分別為![]() ,
,![]() ,
,![]() .
.
由題意,![]() 可能的取值為
可能的取值為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并且
,并且
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
所以![]() 的分布列為
的分布列為
|
|
|
|
|
|
|
|
|
|
|
|
![]() .
.
(3)【解法一】
因為![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,
則該客戶在十年使用期內購買各級濾芯所需總費用的期望值為![]() ;
;
若![]() ,
,![]() ,
,
則該客戶在十年使用期內購買各級濾芯所需總費用的期望值為
![]() .
.
故![]() ,
,![]() 的值分別為
的值分別為![]() ,
,![]() .
.
【解法二】
因為![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,
設該客戶在十年使用期內購買一級濾芯所需總費用為![]() (單位:元),則
(單位:元),則
|
|
|
|
|
|
|
|
![]() .
.
設該客戶在十年使用期內購買二級濾芯所需總費用為![]() (單位:元),則
(單位:元),則
![]() ,
,![]() .
.
所以該客戶在十年使用期內購買各級濾芯所需總費用的期望值為
![]() .
.
若![]() ,
,![]() ,
,
設該客戶在十年使用期內購買一級濾芯所需總費用為![]() (單位:元),則
(單位:元),則
|
|
|
|
|
|
![]() .
.
設該客戶在十年使用期內購買二級濾芯所需總費用為![]() (單位:元),則
(單位:元),則
|
|
|
|
|
|
![]() .
.
所以該客戶在十年使用期內購買各級濾芯所需總費用的期望值為
![]() .
.
故![]() ,
,![]() 的值分別為
的值分別為![]() ,
,![]() .
.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:高中數學 來源: 題型:
【題目】如圖,△ABC為正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中點.求證:

(1)DE=DA;
(2)平面BDM⊥平面ECA;
(3)平面DEA⊥平面ECA.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】伴隨著智能手機的深入普及,支付形式日漸多樣化,打破了傳統支付的局限性和壁壘,有研究表明手機支付的使用比例與人的年齡存在一定的關系,某調研機構隨機抽取了50人,對他們一個月內使用手機支付的情況進行了統計,如下表:

(1)若以“年齡55歲為分界點”,由以上統計數據完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為“使用手機支付”與人的年齡有關;
的把握認為“使用手機支付”與人的年齡有關;

(2)若從年齡在![]() ,
,![]() 內的被調查人中各隨機選取2人進行追蹤調查,記選中的4人中“使用手機支付”的人數為
內的被調查人中各隨機選取2人進行追蹤調查,記選中的4人中“使用手機支付”的人數為![]() .
.
①求隨機變量![]() 的分布列;
的分布列;
②求隨機變量![]() 的數學期望.
的數學期望.
參考數據如下:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
參考格式:![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形,![]() ,
,![]() .
.![]() 是
是![]() 的中點,
的中點,![]() 底面
底面![]() ,
,![]() 在平面
在平面![]() 上的正投影為點
上的正投影為點![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() .
.
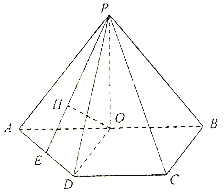
(1)求證:![]() 為
為![]() 中點;
中點;
(2)若![]() ,
,![]() ,在棱
,在棱![]() 上確定一點
上確定一點![]() ,使得
,使得![]() 平面
平面![]() ,并求出
,并求出![]() 與面
與面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某旅游區每年各個月份接待游客的人數近似地滿足周期性規律,因而第![]() 個月從事旅游服務工作的人數
個月從事旅游服務工作的人數![]() 可近似地用函數
可近似地用函數![]() 來刻畫,其中正整數
來刻畫,其中正整數![]() 表示月份且
表示月份且![]() ,例如
,例如![]() 表示1月份,
表示1月份,![]() 和
和![]() 是正整數,
是正整數,![]() ,
,![]() . 統計發現,該地區每年各個月份從事旅游服務工作的人數有以下規律:
. 統計發現,該地區每年各個月份從事旅游服務工作的人數有以下規律:
① 每年相同的月份,該地區從事旅游服務工作的人數基本相同;
② 該地區從事旅游服務工作的人數最多的8月份和最少的2月份相差400人;
③ 2月份該地區從事旅游服務工作的人數為100人,隨后逐月遞增直到8月份達到最多.
(1)試根據已知信息,求![]() 的表達式;
的表達式;
(2)一般地,當該地區從事旅游服務工作的人數在400或400以上時,該地區也進入了一年中的旅游“旺季”,那么,一年中的哪幾個月是該地區的旅游“旺季”?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車因綠色、環保、健康的出行方式,在國內得到迅速推廣.最近,某機構在某地區隨機采訪了10名男士和10名女士,結果男士、女士中分別有7人、6人表示“經常騎共享單車出行”,其他人表示“較少或不選擇騎共享單車出行”.
(1)從這些男士和女士中各抽取一人,求至少有一人“經常騎共享單車出行”的概率;
(2)從這些男士中抽取一人,女士中抽取兩人,記這三人中“經常騎共享單車出行”的人數為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的長軸長是短軸長的2倍,且過點
的長軸長是短軸長的2倍,且過點![]() .
.
⑴求橢圓![]() 的方程;
的方程;
⑵若在橢圓上有相異的兩點![]() (
(![]() 三點不共線),
三點不共線),![]() 為坐標原點,且直線
為坐標原點,且直線![]() ,直線
,直線![]() ,直線
,直線![]() 的斜率滿足
的斜率滿足![]() .
.
(ⅰ)求證: ![]() 是定值;
是定值;
(ⅱ)設![]() 的面積為
的面積為![]() ,當
,當![]() 取得最大值時,求直線
取得最大值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)求函數![]() 的單調區間;
的單調區間;
(Ⅱ)如果對于任意的![]() ,
,![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(III)設函數![]() ,
, ![]() ,過點
,過點![]() 作函數
作函數![]() 的圖象的所有切線,令各切點的橫坐標按從小到大構成數列
的圖象的所有切線,令各切點的橫坐標按從小到大構成數列![]() ,求數列
,求數列![]() 的所有項之和的值.
的所有項之和的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com