
【題目】某地區(qū)對一種新品種小麥在一塊試驗田進(jìn)行試種.從試驗田中抽取![]() 株小麥,測量這些小麥的生長指標(biāo)值,由測量結(jié)果得如下頻數(shù)分布表:
株小麥,測量這些小麥的生長指標(biāo)值,由測量結(jié)果得如下頻數(shù)分布表:
生長指標(biāo)值分組 |
|
|
|
|
|
|
|
頻數(shù) |
|
|
|
|
|
|
|

(1)在相應(yīng)位置上作出這些數(shù)據(jù)的頻率分布直方圖;
(2)求這![]() 株小麥生長指標(biāo)值的樣本平均數(shù)
株小麥生長指標(biāo)值的樣本平均數(shù)![]() 和樣本方差
和樣本方差![]() (同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表);
(同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表);
(3)由直方圖可以認(rèn)為,這種小麥的生長指標(biāo)值![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,其中
,其中![]() 近似為樣本平均數(shù)
近似為樣本平均數(shù)![]() ,
, ![]() 近似為樣本方差
近似為樣本方差![]() .
.
①利用該正態(tài)分布,求![]() ;
;
②若從試驗田中抽取![]() 株小麥,記
株小麥,記![]() 表示這
表示這![]() 株小麥中生長指標(biāo)值位于區(qū)間
株小麥中生長指標(biāo)值位于區(qū)間![]() 的小麥株數(shù),利用①的結(jié)果,求
的小麥株數(shù),利用①的結(jié)果,求![]() .
.
附: ![]() .
.
若![]() ,則
,則![]() ,
,
![]() .
.
【答案】(1)見解析;(2)平均數(shù)200,方差150;(3)①0.6826;②68.26.
【解析】試題分析:(1)根據(jù)題設(shè)中的數(shù)據(jù),即可畫出頻率分布直方圖;
(2)利用平均數(shù)和方差的計算公式,即可求得平均數(shù)![]() ,
, ![]() .
.
(3)①由(1)知![]() ,從而
,從而![]() .
.
②由①知,隨機(jī)變量![]() 服從二項分布,利用公式即可求解期望.
服從二項分布,利用公式即可求解期望.
試題解析:
(1)畫圖.

(2)抽取小麥的生長指標(biāo)值的樣本平均數(shù)![]() 和樣本方差
和樣本方差![]() 分別為
分別為
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]() .
.
(3)①由(1)知![]() ,從而
,從而
![]()
![]()
![]() .
.
②由①知,一株小麥的生長指標(biāo)值位于區(qū)間![]() 的概率為
的概率為![]() ,
,
依題意知![]() ,
,
所以![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)若不過原點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,與直線
兩點,與直線![]() 相較于點
相較于點![]() ,且
,且![]() 是線段
是線段![]() 的中點,求
的中點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
![]() 當(dāng)
當(dāng)![]() 時,畫出函數(shù)的圖像,并寫出使得
時,畫出函數(shù)的圖像,并寫出使得![]() 的所有
的所有![]() 組成的集合.
組成的集合.
![]() 若該函數(shù)的圖像都在
若該函數(shù)的圖像都在![]() 軸的上方,求
軸的上方,求![]() 的取值范圍.
的取值范圍.
![]() 若該函數(shù)在區(qū)間
若該函數(shù)在區(qū)間![]() 上不單調(diào),求
上不單調(diào),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線 (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線 (
(![]() 為參數(shù)),以坐標(biāo)原點為極點,
為參數(shù)),以坐標(biāo)原點為極點, ![]() 軸的正半軸為極軸建立直角坐標(biāo)系.
軸的正半軸為極軸建立直角坐標(biāo)系.
(1)求曲線![]() 的極坐標(biāo)方程,直線
的極坐標(biāo)方程,直線![]() 的普通方程;
的普通方程;
(2)把直線![]() 向左平移一個單位得到直線
向左平移一個單位得到直線![]() ,設(shè)
,設(shè)![]() 與曲線
與曲線![]() 的交點為
的交點為![]() ,
, ![]() ,
, ![]() 為曲線
為曲線![]() 上任意一點,求
上任意一點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在棱長為1的正方體![]() 中,點
中,點![]() 是對角線
是對角線![]() 上的動點(點
上的動點(點![]() 與
與![]() 不重合),則下列結(jié)論正確的是____.
不重合),則下列結(jié)論正確的是____.
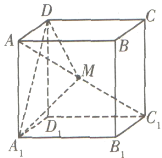
①存在點![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在點![]() ,使得
,使得![]() 平面
平面![]() ;
;
③![]() 的面積不可能等于
的面積不可能等于![]() ;
;
④若![]() 分別是
分別是![]() 在平面
在平面![]() 與平面
與平面![]() 的正投影的面積,則存在點
的正投影的面積,則存在點![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知定義在R上的函數(shù)f(x)對任意實數(shù)x、y恒有f(x)+f(y)=f(x+y),且當(dāng)x>0時,f(x)<0,又f(1)=-![]() .
.
(1)求證:f(x)為奇函數(shù);
(2)求證:f(x)在R上是減函數(shù);
(3)求f(x)在[-3,6]上的最大值與最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的焦點為F,F關(guān)于原點的對稱點為P,過F作
的焦點為F,F關(guān)于原點的對稱點為P,過F作![]() 軸的垂線交拋物線于M,N兩點,給出下列三個結(jié)論:
軸的垂線交拋物線于M,N兩點,給出下列三個結(jié)論:
①![]() 必為直角三角形;
必為直角三角形;
②直線![]() 必與拋物線相切;
必與拋物線相切;
③![]() 的面積為
的面積為![]() .其中正確的結(jié)論是___.
.其中正確的結(jié)論是___.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,點![]() 在拋物線
在拋物線![]() 外,過點
外,過點![]() 作拋物線
作拋物線![]() 的兩切線,設(shè)兩切點分別為
的兩切線,設(shè)兩切點分別為![]() ,
,![]() ,記線段
,記線段![]() 的中點為
的中點為![]() .
.

(Ⅰ)求切線![]() ,
,![]() 的方程;
的方程;
(Ⅱ)證明:線段![]() 的中點
的中點![]() 在拋物線
在拋物線![]() 上;
上;
(Ⅲ)設(shè)點![]() 為圓
為圓![]() 上的點,當(dāng)
上的點,當(dāng)![]() 取最大值時,求點
取最大值時,求點![]() 的縱坐標(biāo).
的縱坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義區(qū)間(a,b),[a,b),(a,b],[a,b]的長度均為![]() ,多個區(qū)間并集的長度為各區(qū)間長度之和,例如,(1,2)
,多個區(qū)間并集的長度為各區(qū)間長度之和,例如,(1,2) ![]() [3,5)的長度d=(2-1)+(5-3)=3. 用[x]表示不超過x的最大整數(shù),記{x}=x-[x],其中
[3,5)的長度d=(2-1)+(5-3)=3. 用[x]表示不超過x的最大整數(shù),記{x}=x-[x],其中![]() .設(shè)
.設(shè)![]() ,
, ![]() ,當(dāng)
,當(dāng)![]() 時,不等式
時,不等式![]() 解集區(qū)間的長度為
解集區(qū)間的長度為![]() ,則
,則![]() 的值為_______.
的值為_______.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com