-1
分析:先利用正弦定理及和角的三角函數,可求cosA的值,進而可求sinA,利用三角形的面積,求得bc.利用向量的數量積公式,即可得到結論.
解答:∵(3b-c)cosA=acosC∴由正弦定理,可得:3sinBcosA-sinCcosA=sinAcosC
∴3sinBcosA=sinAcosC+sinCcosA
∴3sinBcosA=sin(A+C)=sinB
∴cosA=

,sinA=

∵

∴

bcsinA=

bc=

∴bc=3
∵cosA=

,
∴cos<
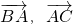
>=-

∴
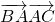
=bccos<
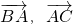
>=-1
故答案為:-1
點評:本題考查正弦定理,考查三角形的面積公式,解題的關鍵是利用正弦定理,進行邊角互化.

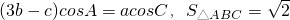 ,則
,則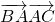 =________.
=________. 閱讀快車系列答案
閱讀快車系列答案