
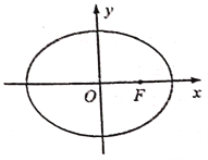
【題目】如圖,在平面直角坐標系xOy中,橢圓C:![]() (a>b>0)經過點(0,
(a>b>0)經過點(0,![]() ),點F是橢圓的右焦點,點F到左頂點的距離和到右準線的距離相等.過點F的直線
),點F是橢圓的右焦點,點F到左頂點的距離和到右準線的距離相等.過點F的直線![]() 交橢圓于M,N兩點.
交橢圓于M,N兩點.
(1)求橢圓C的標準方程;
(2)當MF=2FN時,求直線![]() 的方程;
的方程;
(3)若直線![]() 上存在點P滿足PM·PN=PF2,且點P在橢圓外,證明:點P在定直線上.
上存在點P滿足PM·PN=PF2,且點P在橢圓外,證明:點P在定直線上.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)見解析.
;(3)見解析.
【解析】
(1)由題意,b=![]() ,再由點F到左頂點的距離和到右準線的距離相等,得a+c=
,再由點F到左頂點的距離和到右準線的距離相等,得a+c=![]() ,結合隱含條件解得a=2,c=1,則橢圓方程可求;
,結合隱含條件解得a=2,c=1,則橢圓方程可求;
(2)當直線l與x軸重合時,求得MF=3NF,不合題意;當直線l與x軸不重合時,設直線l的方程為x=my+1,M(x1,y1),N(x2,y2),聯立直線方程與橢圓方程,化為關于y的一元二次方程,由根與系數的關系及MF=2FN求得m值,則直線方程可求;
(3)當直線l的斜率為0時,設P(x0,y0),由PMPN=PF2,求得![]() ,當直線l的斜率不為0時,由(2)中的根與系數的關系及PMPN=PF2,求得
,當直線l的斜率不為0時,由(2)中的根與系數的關系及PMPN=PF2,求得![]() ,代入直線方程得
,代入直線方程得![]() ,由此可得點P在定直線
,由此可得點P在定直線![]() 上.
上.
(1)設橢圓的截距為2c,由題意,b=![]() ,
,
由點F到左頂點的距離和到右準線的距離相等,得a+c=![]() ,
,
又a2=b2+c2,聯立解得a=2,c=1.
∴橢圓C的標準方程為![]() ;
;
(2)當直線l與x軸重合時,M(﹣2,0),N(2,0),此時MF=3NF,不合題意;
當直線l與x軸不重合時,設直線l的方程為x=my+1,M(x1,y1),N(x2,y2),
聯立 ,得(3m2+4)y2+6my﹣9=0.△=36m2+36(m2+4)>0.
,得(3m2+4)y2+6my﹣9=0.△=36m2+36(m2+4)>0.
![]() ①,
①,![]() ②,由MF=2FN,得y1=﹣2y2③,
②,由MF=2FN,得y1=﹣2y2③,
聯立①③得,![]() ,
,
代入②得, ,解得
,解得![]() .∴直線方程為
.∴直線方程為![]() ;
;
(3)當直線l的斜率為0時,則M(2,0),N(﹣2,0),設P(x0,y0),
則PMPN=|(x0﹣2)(x0+2)|,∵點P在橢圓外,∴x0﹣2,x0+2同號,
又![]() ,解得
,解得![]() .
.
當直線l的斜率不為0時,由(2)知,![]() ,
,
![]() .
.
∵點P在橢圓外,∴y1﹣y0,y2﹣y0同號,
∴PMPN=(1+m2)(y1﹣y0)(y2﹣y0)=![]()
![]() ,
,
整理得![]() ,代入直線方程得
,代入直線方程得![]() .∴點P在定直線
.∴點P在定直線![]() 上.
上.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在平面上給定相異兩點A,B,設P點在同一平面上且滿足![]() ,當
,當![]() 且
且![]() 時,P點的軌跡是一個圓,這個軌跡最先由古希臘數學家阿波羅尼斯發現,故我們稱這個圓為阿波羅尼斯圓,現有雙曲線
時,P點的軌跡是一個圓,這個軌跡最先由古希臘數學家阿波羅尼斯發現,故我們稱這個圓為阿波羅尼斯圓,現有雙曲線![]() (
(![]() ,
,![]() ),A,B為雙曲線的左、右頂點,C,D為雙曲線的虛軸端點,動點P滿足
),A,B為雙曲線的左、右頂點,C,D為雙曲線的虛軸端點,動點P滿足 ,
,![]() 面積的最大值為
面積的最大值為![]() ,
,![]() 面積的最小值為4,則雙曲線的離心率為______.
面積的最小值為4,則雙曲線的離心率為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() (
(![]() )經過點
)經過點![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 有兩個不同的交點
有兩個不同的交點![]() 、
、![]() ,直線
,直線![]() 交
交![]() 軸于
軸于![]() ,直線
,直線![]() 交
交![]() 軸于
軸于![]() .
.
(1)若直線![]() 過點
過點![]() ,求直線
,求直線![]() 的斜率的取值范圍;
的斜率的取值范圍;
(2)若直線![]() 過點
過點![]() ,設
,設![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若直線![]() 過拋物線
過拋物線![]() 的焦點
的焦點![]() ,交
,交![]() 軸于點
軸于點![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數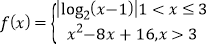 若方程f(x)=m有4個不同的實根x1,x2,x3,x4,且x1<x2<x3<x4,則(
若方程f(x)=m有4個不同的實根x1,x2,x3,x4,且x1<x2<x3<x4,則(![]() )(x3+x4)=( )
)(x3+x4)=( )
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,
,![]() 是橢圓
是橢圓![]() 上一點,
上一點,![]() 軸,
軸,![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,
,![]() 為坐標原點,且
為坐標原點,且![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在合作學習小組的一次活動中,甲、乙、丙、丁、戊五位同學被隨機地分配承擔![]() ,
,![]() ,
,![]() ,
,![]() 四項不同的任務,每個同學只能承擔一項任務.
四項不同的任務,每個同學只能承擔一項任務.
(1)若每項任務至少安排一位同學承擔,求甲、乙兩人不同時承擔同一項任務的概率;
(2)設這五位同學中承擔任務![]() 的人數為隨機變量
的人數為隨機變量![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com