
【題目】已知![]() ,
,![]() 為拋物線
為拋物線![]() 上的相異兩點,且
上的相異兩點,且![]() .
.

(1)若直線![]() 過
過![]() ,求
,求![]() 的值;
的值;
(2)若直線![]() 的垂直平分線交
的垂直平分線交![]() 軸與點
軸與點![]() ,求
,求![]() 面積的最大值.
面積的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)設直線![]() 的方程為
的方程為![]() ,聯立拋物線方程,運用韋達定理和中點坐標公式,以及弦長公式,計算可得所求值;
,聯立拋物線方程,運用韋達定理和中點坐標公式,以及弦長公式,計算可得所求值;
(2)設線段![]() 的中點為
的中點為![]() ,
,![]() ,運用中點坐標公式和直線的斜率公式,以及直線方程,可得
,運用中點坐標公式和直線的斜率公式,以及直線方程,可得![]() 的坐標,
的坐標,
設出直線![]() 的方程代入拋物線方程,運用韋達定理,以及弦長公式和點到直線的距離公式,化簡整理,結合基本不等式可得所求最大值.
的方程代入拋物線方程,運用韋達定理,以及弦長公式和點到直線的距離公式,化簡整理,結合基本不等式可得所求最大值.
解:(1)當垂直于![]() 軸或斜率為零時,顯然不符合題意,所以可設直線
軸或斜率為零時,顯然不符合題意,所以可設直線![]() 的方程為
的方程為![]() ,
,
代入方程![]() ,得
,得![]()
故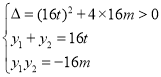
![]() ,
,
結合![]() 解得
解得![]() .
.
因此,![]() .
.
(2)設線段![]() 的中點為
的中點為![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,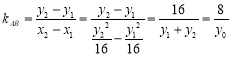 .
.
線段![]() 的垂直平分線的方程是
的垂直平分線的方程是![]() ,①
,①
由題意知![]() ,
,![]() 是①的一個解,
是①的一個解,
所以線段![]() 的垂直平分線與
的垂直平分線與![]() 軸的交點
軸的交點![]() 為定點,
為定點,
且點![]() 坐標為
坐標為![]() .
.
直線![]() 的方程為
的方程為![]() ,
,
即![]() ,②
,②
②代入![]() 得
得![]() ,即
,即![]() ,③
,③
依題意,![]() ,
,![]() 是方程③的兩個實根,且
是方程③的兩個實根,且![]() ,
,
所以△![]() ,即
,即![]() .
.![]() ,
,![]() ,
,
![]()
![]() ,
,
點![]() 到線段
到線段![]() 的距離
的距離![]() ,
,
![]() .
.
當且僅當![]() ,即
,即![]() 時,上式取得等號.
時,上式取得等號.
所以![]() 面積的最大值為
面積的最大值為![]() .
.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案科目:高中數學 來源: 題型:
【題目】現要完成下列三項抽樣調查:①從![]() 罐奶粉中抽取
罐奶粉中抽取![]() 罐進行食品安全衛生檢查;②高二年級有
罐進行食品安全衛生檢查;②高二年級有![]() 名學生,為調查學生的學習情況抽取一個容量為
名學生,為調查學生的學習情況抽取一個容量為![]() 的樣本;③從某社區
的樣本;③從某社區![]() 戶高收入家庭,
戶高收入家庭,![]() 戶中等收入家庭,
戶中等收入家庭,![]() 戶低收入家庭中選出
戶低收入家庭中選出![]() 戶進行消費水平調查.以下各調查方法較為合理的是( )
戶進行消費水平調查.以下各調查方法較為合理的是( )
A.①系統抽樣,②簡單隨機抽樣,③分層抽樣
B.①簡單隨機抽樣,②分層抽樣,③系統抽樣
C.①分層抽樣,②系統抽樣,③簡單隨機抽樣
D.①簡單隨機抽樣,②系統抽樣,③分層抽樣
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校調查喜歡“統計”課程是否與性別有關,隨機抽取了55個學生,得到統計數據如表:
喜歡 | 不喜歡 | 總計 | |
男生 | 20 | ||
女生 | 20 | ||
總計 | 30 | 55 |
(1)完成表格的數據;
(2)判斷是否在犯錯誤的概率不超過0.005的前提下認為喜歡“統計”課程與性別有關?
參考公式:![]()
| 0.025 | 0.01 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,四邊形![]() 是矩形,點
是矩形,點![]() ,點
,點![]() ,點
,點![]() .以點
.以點![]() 為中心,順時針旋轉矩形
為中心,順時針旋轉矩形![]() ,得到矩形
,得到矩形![]() ,點
,點![]() 的對應點分別為
的對應點分別為![]() .
.

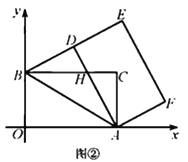
(1)如圖①,當點![]() 落在
落在![]() 邊上時,求點
邊上時,求點![]() 的坐標;
的坐標;
(2)如圖②,當點![]() 落在線段
落在線段![]() 上時,
上時,![]() 與
與![]() 交于點
交于點![]() .
.
①求證![]() ;②求點
;②求點![]() 的坐標.
的坐標.
(3)記![]() 為矩形
為矩形![]() 對角線的交點,
對角線的交點,![]() 為
為![]() 的面積,求
的面積,求![]() 的取值范圍(直接寫出結果即可).
的取值范圍(直接寫出結果即可).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小明每天上學都需要經過一個有交通信號燈的十字路口.已知十字路口的交通信號燈綠燈亮的時間為40秒,黃燈5秒,紅燈45秒.如果小明每天到路口的時間是隨機的,則小明上學時到十字路口需要等待的時間不少于20秒的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 均為大于1的整數,
均為大于1的整數, ![]() 為n個不超過m的互不相同的正整數,且
為n個不超過m的互不相同的正整數,且![]() 互素.證明:對任意實數x,均存在一個
互素.證明:對任意實數x,均存在一個![]() ,使得
,使得![]() ,其中
,其中![]() 表示實數r到與其最近的整數的距離。
表示實數r到與其最近的整數的距離。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商家通過市場調研,發現某商品的銷售價格y(元/件)和銷售量x(件)有關,其關系可用圖中的折線段![]() 表示(不包含端點A).
表示(不包含端點A).

(1)把y表示成x的函數;
(2)若該商品進貨價格為12元/件,則商家賣出多少件時可以獲得最大利潤?最大利潤為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋子中有四個小球,分別寫有“美、麗、中、國”四個字,有放回地從中任取一個小球,直到“中”“國”兩個字都取到就停止,用隨機模擬的方法估計恰好在第三次停止的概率.利用電腦隨機產生0到3之間取整數值的隨機數,分別用0,1,2,3代表“中、國、美、麗”這四個字,以每三個隨機數為一組,表示取球三次的結果,經隨機模擬產生了以下18組隨機數:
232 321 230 023 123 021 132 220 001
231 130 133 231 031 320 122 103 233
由此可以估計,恰好第三次就停止的概率為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com