
【題目】對于函數![]() 、
、![]() 、
、![]() ,如果存在實數
,如果存在實數![]() 使得
使得![]() ,那么稱
,那么稱![]() 為
為![]() 、
、![]() 的生成函數.
的生成函數.
(1) 下面給出兩組函數, ![]() 是否分別為
是否分別為![]() 、
、![]() 的生成函數?并說明理由;
的生成函數?并說明理由;
第一組: ![]() ,
, ![]() ,
, ![]()
第二組: ![]() ,
, ![]() ,
, ![]() ;
;
(2) 設![]() ,
, ![]() ,
, ![]() ,生成函數
,生成函數![]() .若不等式
.若不等式![]() 在
在![]() 上有解,求實數
上有解,求實數![]() 的取值范圍;
的取值范圍;
(3) 設![]() ,
, ![]() ,取
,取![]() ,生成函數
,生成函數![]() 圖像的最低點坐標為
圖像的最低點坐標為![]() .若對于任意正實數
.若對于任意正實數![]() ,且
,且![]() ,試問是否存在最大的常數
,試問是否存在最大的常數![]() ,使
,使![]() 恒成立?如果存在,求出這個
恒成立?如果存在,求出這個![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
【答案】(1)見解析 (2) ![]() (3)
(3) ![]() 為289
為289
【解析】試題分析:(1)由條件利用生成函數的定義,判斷生成函數![]() 是否分別為是
是否分別為是![]() 、
、![]() 的生成函數,從而得出結論;(2)
的生成函數,從而得出結論;(2)![]() 有解等價于
有解等價于![]() 在
在![]() 上有解,只需
上有解,只需![]() 小于函數
小于函數![]() 在
在![]() 的最大值即可;(3)先求出函數
的最大值即可;(3)先求出函數![]() 的最小值為289,只需
的最小值為289,只需![]() 即可.
即可.
試題解析:(1)第一組: ![]() 是
是![]() 、
、![]() 的生成函數,因為存在
的生成函數,因為存在![]() 使
使![]()
第二組: ![]() 不是
不是![]() 、
、![]() 的生成函數,因為若存在
的生成函數,因為若存在![]() 使得
使得![]() ,則有
,則有![]()
![]()
故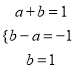 ,而此方程無解,所以
,而此方程無解,所以![]() 不是
不是![]() 、
、![]() 的生成函數 .
的生成函數 .
(2) 依題意,有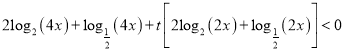 在
在![]() 上有解
上有解
化簡得: ![]() 即
即![]() 在
在![]() 上有解
上有解
函數![]() 在
在![]() 的最大值為
的最大值為![]()
故實數![]() 的取值范圍為
的取值范圍為![]()
(3) 存在最大的常數![]() 為289
為289
依題意, ![]() ,由
,由![]() 當且僅當
當且僅當![]() 即
即![]() 時等號成立得:
時等號成立得:
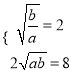 ,解得:
,解得: ![]() ,故
,故![]()
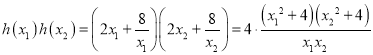
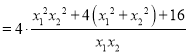
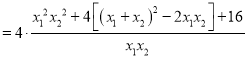
![]()
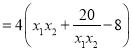
正數![]() ,滿足/span>
,滿足/span>![]() ,故
,故![]() 當且僅當
當且僅當![]() 時等號成立
時等號成立
函數![]() 的最小值為289,故最大的常數
的最小值為289,故最大的常數![]() 為289.
為289.
【方法點晴】本題主要考查對數的運算、二次函數的性質以及不等式恒成立問題,屬于難題.不等式恒成立問題常見方法:① 分離參數![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 數形結合(
即可);② 數形結合(![]() 圖象在
圖象在![]() 上方即可);③ 討論最值
上方即可);③ 討論最值![]() 或
或![]() 恒成立;④ 討論參數.本題是利用方法 ① 求得
恒成立;④ 討論參數.本題是利用方法 ① 求得![]() 的最大值.
的最大值.


科目:高中數學 來源: 題型:
【題目】現有紅、黃、藍三種顏色小旗各2面,將他們排成3行2列,要求每行及每列的顏色均互不相同,則不同的排列方法共有( )
A. 12種 B. 18種 C. 24種 D. 36種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面給出了四個類比推理: (1.)由“若a,b,c∈R則(ab)c=a(bc)”類比推出“若a,b,c為三個向量則( ![]()
![]() )
) ![]() =
= ![]() (
( ![]()
![]() )”;
)”;
(2.)“a,b為實數,若a2+b2=0則a=b=0”類比推出“z1 , z2為復數,若 ![]() ”;
”;
(3.)“在平面內,三角形的兩邊之和大于第三邊”類比推出“在空間中,四面體的任意三個面的面積之和大于第四個面的面積”;
(4.)“在平面內,過不在同一條直線上的三個點有且只有一個圓”類比推出“在空間中,過不在同一個平面上的四個點有且只有一個球”.
上述四個推理中,結論正確的個數有( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖放置的邊長為1的正方形![]() 沿
沿![]() 軸滾動(向右為順時針,向左為逆時針).設頂點
軸滾動(向右為順時針,向左為逆時針).設頂點![]() 的軌跡方程是
的軌跡方程是![]() ,則關于
,則關于![]() 的最小正周期
的最小正周期![]() 及
及![]() 在其兩個相鄰零點間的圖像與x軸所圍區域的面積S的正確結論是( )
在其兩個相鄰零點間的圖像與x軸所圍區域的面積S的正確結論是( )
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓M過定點P(1,0),且與直線x=﹣1相切.
(1)求動圓圓心M的軌跡C的方程;
(2)設A、B是軌跡C上異于原點O的兩點,且 ![]() =0,求證:直線AB過定點.
=0,求證:直線AB過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)= ![]() 是定義在區間(﹣1,1)上的奇函數,且f(2)=
是定義在區間(﹣1,1)上的奇函數,且f(2)= ![]() ,
,
(1)確定函數f(x)的解析式;
(2)用定義法證明f(x)在區間(﹣1,1)上是增函數;
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|x2﹣3x<0},B={x|(x+2)(4﹣x)≥0},C={x|a<x≤a+1}.
(1)求A∩B;
(2)若B∪C=B,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com