
【題目】在三棱臺![]() 中,
中,![]() 為正三角形,
為正三角形,![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
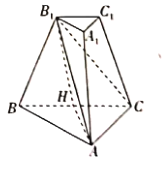
(1)若![]() 為
為![]() 中點,求證:
中點,求證:![]() 平面
平面![]() ;
;
(2)求![]() 到平面
到平面![]() 的距離.
的距離.
 名校提分一卷通系列答案
名校提分一卷通系列答案 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的右焦點為
的右焦點為![]() ,短軸長為2,過定點
,短軸長為2,過定點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于不同的兩點
于不同的兩點![]() 、
、![]() (點
(點![]() 在點
在點![]() ,
,![]() 之間).
之間).
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(3)若射線![]() 交橢圓
交橢圓![]() 于點
于點![]() (
(![]() 為原點),求
為原點),求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年1月31日晚上月全食的過程分為初虧、食既、食甚、生光、復圓五個階段,月食的初虧發生在19時48分,20時51分食既,食甚時刻為21時31分,22時08分生光,直至23時12分復圓.全食伴隨有藍月亮和紅月亮,全食階段的“紅月亮”將在食甚時刻開始,生光時刻結東,一市民準備在19:55至21:56之間的某個時刻欣賞月全食,則他等待“紅月亮”的時間不超過30分鐘的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C; y2 =2x的焦點為F,準線為l, P為拋物線C上異于頂點的動點.
(1)過點P作準線1的垂線,垂足為H,若△PHF與△POF的面積之比為2:1,求點P的坐標;
(2)過點M(![]() ,0)任作一條直線 m與拋物線C交于不同的兩點A, B.若兩直線PA, PB 斜率之和為2,求點P的坐標.
,0)任作一條直線 m與拋物線C交于不同的兩點A, B.若兩直線PA, PB 斜率之和為2,求點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年某開發區一家汽車生產企業計劃引進一批新能源汽車制造設備,通過市場分析,全年需投入固定成本3000萬元,每生產x(百輛),需另投入成本![]() 萬元,且
萬元,且 ,由市場調研知,每輛車售價6萬元,且全年內生產的車輛當年能全部銷售完.
,由市場調研知,每輛車售價6萬元,且全年內生產的車輛當年能全部銷售完.
(1)求出2019年的利潤![]() (萬元)關于年產量x(百輛)的函數關系式;(利潤=銷售額
(萬元)關于年產量x(百輛)的函數關系式;(利潤=銷售額![]() 成本)
成本)
(2)2019年產量為多少(百輛)時,企業所獲利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,![]() 是某海灣旅游區的一角,其中
是某海灣旅游區的一角,其中![]() ,為了營造更加優美的旅游環境,旅游區管委會決定在直線海岸
,為了營造更加優美的旅游環境,旅游區管委會決定在直線海岸![]() 和
和![]() 上分別修建觀光長廊
上分別修建觀光長廊![]() 和AC,其中
和AC,其中![]() 是寬長廊,造價是
是寬長廊,造價是![]() 元/米,
元/米,![]() 是窄長廊,造價是
是窄長廊,造價是![]() 元/米,兩段長廊的總造價為120萬元,同時在線段
元/米,兩段長廊的總造價為120萬元,同時在線段![]() 上靠近點
上靠近點![]() 的三等分點
的三等分點![]() 處建一個觀光平臺,并建水上直線通道
處建一個觀光平臺,并建水上直線通道![]() (平臺大小忽略不計),水上通道的造價是
(平臺大小忽略不計),水上通道的造價是![]() 元/米.
元/米.
(1) 若規劃在三角形![]() 區域內開發水上游樂項目,要求
區域內開發水上游樂項目,要求![]() 的面積最大,那么
的面積最大,那么![]() 和
和![]() 的長度分別為多少米?
的長度分別為多少米?
(2) 在(1)的條件下,建直線通道![]() 還需要多少錢?
還需要多少錢?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設S、T是R的兩個非空子集,如果函數![]() 滿足:①
滿足:①![]() ;②對任意
;②對任意![]() ,
,![]() ,當
,當![]() 時,恒有
時,恒有![]() ,那么稱函數
,那么稱函數![]() 為集合S到集合T的“保序同構函數”.
為集合S到集合T的“保序同構函數”.
(1)試寫出集合![]() 到集合R的一個“保序同構函數”;
到集合R的一個“保序同構函數”;
(2)求證:不存在從集合Z到集合Q的“保序同構函數”;
(3)已知![]() 是集合
是集合![]() 到集合
到集合![]() 的“保序同構函數”,求s和t的最大值.
的“保序同構函數”,求s和t的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在中國足球超級聯賽某一季的收官階段中,廣州恒大淘寶、北京中赫國安、上海上港、山東魯能泰山分別積分59分、58分、56分、50分,四家俱樂部都有機會奪冠.A,B,C三個球迷依據四支球隊之前比賽中的表現,結合自已的判斷,對本次聯賽的冠軍進行如下猜測:![]() 猜測冠軍是北京中赫國安或山東魯能泰山;
猜測冠軍是北京中赫國安或山東魯能泰山;![]() 猜測冠軍一定不是上海上港和山東魯能泰山;
猜測冠軍一定不是上海上港和山東魯能泰山;![]() 猜測冠軍是廣州恒大淘寶或北京中赫國安.聯賽結束后,發現A,B,C三人中只有一人的猜測是正確的,則冠軍是( )
猜測冠軍是廣州恒大淘寶或北京中赫國安.聯賽結束后,發現A,B,C三人中只有一人的猜測是正確的,則冠軍是( )
A.廣州恒大淘寶B.北京中赫國安C.上海上港D.山東魯能泰山
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知甲盒內有大小相同的2個紅球和3個黑球,乙盒內有大小相同的3個紅球和3個黑球,現從甲,乙兩個盒內各取2個球.
(1)求取出的4個球中恰有1個紅球的概率;
(2)設ξ為取出的4個球中紅球的個數,求ξ的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com