
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在區間
在區間![]() 上的值域.
上的值域.
(2)對于任意![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1) 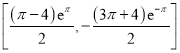 (2)
(2) ![]()
【解析】試題分析:(1)先求導數,再求![]() 導數,得
導數,得![]() 從而確定
從而確定![]() ,再根據
,再根據![]() 單調性得值域(2)先整理不等式得
單調性得值域(2)先整理不等式得![]() ,轉化為函數
,轉化為函數![]() 在區間
在區間![]() 為增函數,再轉化為對應函數導數恒非負,分離變量得
為增函數,再轉化為對應函數導數恒非負,分離變量得![]() 最小值,最后利用導數求函數
最小值,最后利用導數求函數![]() 單調性,得最值,即得實數
單調性,得最值,即得實數![]() 的取值范圍.
的取值范圍.
試題解析:(1)當![]() 時,
時, ![]() ,
,
![]() ,
,
令![]() ,有
,有![]() ,
,
當![]() 時,
時, ![]() ,
,
當![]() 時
時![]() ,
,
得![]() ,解得:
,解得: ![]() ,
,
故當![]() 時,函數
時,函數![]() 單調遞減,當
單調遞減,當![]() 時,函數
時,函數![]() 單調遞增,
單調遞增,
所以當![]() 時,
時, ![]() ,可得
,可得![]() ,
,
函數![]() 在區間
在區間![]() 上單調遞減,
上單調遞減,
![]() ,
,
![]() ,
,
故函數![]() 在區間
在區間![]() 上的值域為
上的值域為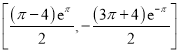 .
.
(2)由![]() ,有
,有![]() ,
,
故![]() 可化為
可化為![]() ,
,
整理為: ![]() ,
,
即函數![]() 在區間
在區間![]() 為增函數,
為增函數,
![]()
![]() ,
,
![]() ,故當
,故當![]() 時,
時, ![]() ,
,
即![]() ,
,
①當![]() 時,
時, ![]() ;
;
②當![]() 時,整理為:
時,整理為: ![]() ,
,
令![]() ,有
,有![]()
![]() ,
,
當![]() ,
, ![]() ,
, ![]() ,有
,有![]() ,
,
當![]() 時,由
時,由![]() ,有
,有![]()
![]() ,可得
,可得![]() ,
,
由上知![]() 時,函數
時,函數![]() 單調遞減,
單調遞減,
故![]() ,
,
故有: ![]() ,可得
,可得![]() .
.


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線C的參數方程為
中,曲線C的參數方程為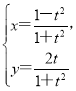 (t為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線
(t為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求C的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)求C上的點到![]() 距離的最大值.
距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】上海市松江區天馬山上的“護珠塔”因其傾斜度超過意大利的比薩斜塔而號稱“世界第一斜塔”.興趣小組同學實施如下方案來測量塔的傾斜度和塔高:如圖,記O點為塔基、P點為塔尖、點P在地面上的射影為點H.在塔身OP射影所在直線上選點A,使仰角∠HAP=45°,過O點與OA成120°的地面上選B點,使仰角∠HPB=45°(點A、B、O都在同一水平面上),此時測得∠OAB=27°,A與B之間距離為33.6米.試求:
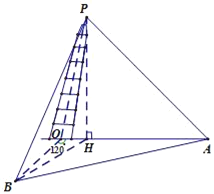
(1)塔高(即線段PH的長,精確到0.1米);
(2)塔身的傾斜度(即PO與PH的夾角,精確到0.1°).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了促進某產品的銷售,隨機調查了該產品的月銷售單價x(單位:元/件)及相應月銷量y(單位:萬件),對近5個月的月銷售單價![]() 和月銷售量
和月銷售量![]() 的數據進行了統計,得到如下數表:
的數據進行了統計,得到如下數表:
月銷售單價 | 8 | 8.5 | 9 | 9.5 | 10 |
月銷售量 | 11 | 10 | 8 | 6 | 5 |
(1)建立![]() 關于
關于![]() 的回歸直線方程;
的回歸直線方程;
(2)該公司年底開展促銷活動,當月銷售單價為7元/件時,其月銷售量達到14.8萬件,若由回歸直線方程得到的預測數據與此次促銷活動的實際數據之差的絕對值不超過0.5萬件,則認為所得到的回歸直線方程是理想的,試問(1)中得到的回歸直線方程是否理想?
(3)根據(1)的結果,若該產品成本是5元/件,月銷售單價![]() 為何值時,公司月利潤的預報值最大?(注:利潤=銷售收入-成本).
為何值時,公司月利潤的預報值最大?(注:利潤=銷售收入-成本).
參考公式:回歸直線方程![]() ,其中
,其中 ,
,![]()
參考數據:![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中國詩詞大會》是由CCTV-10自主研發的一檔大型文化益智節目,以“賞中華詩詞,尋文化基因品生活之美”為宗旨,帶動全民重溫經典、從古人的智慧和情懷中汲取營養、涵養心靈,節目廣受好評還因為其頗具新意的比賽規則:每場比賽,106位挑戰者全部參賽,分為單人追逐賽和擂主爭霸賽兩部分單人追逐賽的最終優勝者作為攻擂者與守擂擂主進行比拼,競爭該場比賽的擂主,擂主爭霸賽以搶答的形式展開,共九道題,搶到并回答正確者得一分,答錯則對方得一分,先得五分者獲勝,成為本場擂主,比賽結束已知某場擂主爭霸賽中,攻擂者與守擂擂主都參與每一次搶題且兩人搶到每道題的概率都是![]() ,攻擂者與守擂擂主正確回答每道題的概率分別為
,攻擂者與守擂擂主正確回答每道題的概率分別為![]() ,
,![]() ,且兩人各道題是否回答正確均相互獨立.
,且兩人各道題是否回答正確均相互獨立.
(1)比賽開始,求攻擂者率先得一分的概率;
(2)比賽進行中,攻擂者暫時以![]() 領先,設兩人共繼續搶答了
領先,設兩人共繼續搶答了![]() 道題比賽結束,求隨機變量
道題比賽結束,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地政府為改善居民的住房條件,集中建設一批經適樓房.用了1400萬元購買了一塊空地,規劃建設8幢樓,要求每幢樓的面積和層數等都一致,已知該經適房每幢樓每層建筑面積均為250平方米,第一層建筑費用是每平方米3000元,從第二層開始,每一層的建筑費用比其下面一層每平方米增加80元.
(1)若該經適樓房每幢樓共![]() 層,總開發費用為
層,總開發費用為![]() 萬元,求函數
萬元,求函數![]() 的表達式(總開發費用=總建筑費用+購地費用);
的表達式(總開發費用=總建筑費用+購地費用);
(2)要使該批經適房的每平方米的平均開發費用最低,每幢樓應建多少層?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 和
和![]() 均是等腰直角三角形,
均是等腰直角三角形,![]() ,
,![]() ,
,![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點.
的中點.
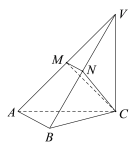
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求證:![]() ;
;
(Ⅲ)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com