
【題目】《中國詩詞大會》是由CCTV-10自主研發的一檔大型文化益智節目,以“賞中華詩詞,尋文化基因品生活之美”為宗旨,帶動全民重溫經典、從古人的智慧和情懷中汲取營養、涵養心靈,節目廣受好評還因為其頗具新意的比賽規則:每場比賽,106位挑戰者全部參賽,分為單人追逐賽和擂主爭霸賽兩部分單人追逐賽的最終優勝者作為攻擂者與守擂擂主進行比拼,競爭該場比賽的擂主,擂主爭霸賽以搶答的形式展開,共九道題,搶到并回答正確者得一分,答錯則對方得一分,先得五分者獲勝,成為本場擂主,比賽結束已知某場擂主爭霸賽中,攻擂者與守擂擂主都參與每一次搶題且兩人搶到每道題的概率都是![]() ,攻擂者與守擂擂主正確回答每道題的概率分別為
,攻擂者與守擂擂主正確回答每道題的概率分別為![]() ,
,![]() ,且兩人各道題是否回答正確均相互獨立.
,且兩人各道題是否回答正確均相互獨立.
(1)比賽開始,求攻擂者率先得一分的概率;
(2)比賽進行中,攻擂者暫時以![]() 領先,設兩人共繼續搶答了
領先,設兩人共繼續搶答了![]() 道題比賽結束,求隨機變量
道題比賽結束,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
【答案】(1)![]() (2)答案見解析
(2)答案見解析
【解析】
(1)由題意可知:每道題的搶答中,記攻擂者得一分為事件![]() ,
,![]() 發生有兩種可能:搶到題且答對,對方搶到題且答錯,即可求得攻擂者率先得一分的概率;
發生有兩種可能:搶到題且答對,對方搶到題且答錯,即可求得攻擂者率先得一分的概率;
(2)由(1)知,在每道題的搶答中攻擂者與守擂擂主得一分的概率分別為![]() ,
,![]() .根據比賽規則,
.根據比賽規則,![]() 的所有可能取值分別為
的所有可能取值分別為![]() ,求出
,求出![]() ,
,![]() 和
和![]() ,即可求得隨機變量
,即可求得隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
(1)每道題的搶答中,記攻擂者得一分為事件![]() .
.
![]() 發生有兩種可能:搶到題且答對,對方搶到題且答錯,
發生有兩種可能:搶到題且答對,對方搶到題且答錯,
![]()
![]()
![]() 比賽開始,求攻擂者率先得一分的概率為:
比賽開始,求攻擂者率先得一分的概率為:![]() .
.
(2)由(1)知,在每道題的搶答中攻擂者與守擂擂主得一分的概率分別為![]() ,
,![]()
根據比賽規則,![]() 的所有可能取值分別為
的所有可能取值分別為![]() ,
,
則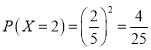
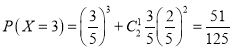
![]()
![]() 的分布列為:
的分布列為:
| 2 | 3 | 4 |
|
|
|
|
![]()
![]() .
.


科目:高中數學 來源: 題型:
【題目】給出下列命題:
(1)存在實數![]() 使
使![]() ;
;
(2)直線![]() 是函數
是函數![]() 圖象的一條對稱軸;
圖象的一條對稱軸;
(3)![]() (
(![]() )的值域是
)的值域是![]() ;
;
(4)若![]() ,
,![]() 都是第一象限角,且
都是第一象限角,且![]() ,則
,則![]() .
.
其中正確命題的序號為( )
A.(1)(2)B.(2)(3)C.(3)(4)D.(1)(4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,
,![]() 是兩條不同的直線,
是兩條不同的直線,![]() ,
,![]() ,
,![]() 是三個不同的平面,給出下列四個命題:
是三個不同的平面,給出下列四個命題:
①若![]() ,
,![]() ,則
,則![]()
②若![]() ,
,![]() ,
,![]() ,則
,則![]()
③若![]() ,
,![]() ,則
,則![]()
④若![]() ,
,![]() ,則
,則![]()
其中正確命題的序號是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合![]() ,若對于任意實數對
,若對于任意實數對![]() ,存在
,存在![]() ,使
,使![]() 成立,則稱集合
成立,則稱集合![]() 是“垂直對點集” .給出下列四個集合:
是“垂直對點集” .給出下列四個集合:
① ![]() ;
;
②![]() ;
;
③ ![]() ;
;
④![]() .
.
其中是“垂直對點集”的序號是( ).
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設曲線![]() 上一點
上一點![]() 到焦點的距離為3.
到焦點的距離為3.
(1)求曲線C方程;
(2)設P,Q為曲線C上不同于原點O的任意兩點,且滿足以線段PQ為直徑的圓過原點O,試問直線PQ是否恒過定點?若恒過定點,求出定點坐標;若不恒過定點,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 在
在![]() 上有定義,實數
上有定義,實數![]() 和
和![]() 滿足
滿足![]() .若
.若![]() 在區間
在區間![]() 上不存在最小值,則稱
上不存在最小值,則稱![]() 在區間
在區間![]() 上具有性質P.
上具有性質P.
(1)當![]() ,且
,且![]() 在區間
在區間![]() 上具有性質P,求常數C的取值范圍;
上具有性質P,求常數C的取值范圍;
(2)已知![]() ,且當
,且當![]() 時,
時,![]() ,判別
,判別![]() 在區間
在區間![]() 上是否具有性質P;
上是否具有性質P;
(3)若對于滿足![]() 的任意實數
的任意實數![]() 和
和![]() ,
,![]() 在區間
在區間![]() 上具有性質P,且對于任意
上具有性質P,且對于任意![]() ,當
,當![]() 時,有:
時,有:![]() ,證明:當
,證明:當![]() 時,
時,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com