
已知正四棱柱 中,
中, .
.
(1)求證: ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)在線段 上是否存在點
上是否存在點 ,使得平面
,使得平面
 平面
平面 ,若存在,求出
,若存在,求出 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
(1)詳見解析;(2)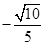 (3)存在,
(3)存在,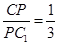
解析試題分析:(1)可證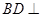 平面
平面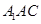 ,從而可得
,從而可得 。(2)(空間向量法)以
。(2)(空間向量法)以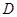 為原點建立空間直角坐標系
為原點建立空間直角坐標系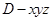 ,如圖。根據邊長可得各點的坐標,從而可得各向量的坐標,根據向量垂直數量積為0可求平面
,如圖。根據邊長可得各點的坐標,從而可得各向量的坐標,根據向量垂直數量積為0可求平面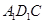 的法向量,由(1)知
的法向量,由(1)知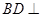 平面
平面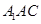 ,所以
,所以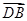 即為平面
即為平面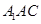 的法向量,先求兩法向量所成角的余弦值,但應注意兩法向量所成的角與二面角的平面角相等或互補,觀察可知此二面角為鈍角,所以此二面角的余弦值應為負數。(3)設
的法向量,先求兩法向量所成角的余弦值,但應注意兩法向量所成的角與二面角的平面角相等或互補,觀察可知此二面角為鈍角,所以此二面角的余弦值應為負數。(3)設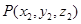 為線段
為線段 上一點,且
上一點,且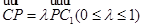 ,根據向量共線,可用
,根據向量共線,可用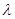 表示出點
表示出點 坐標。分別求兩個面的法向量,兩面垂直,則兩法向量也垂直,即數量積為0,從而可得
坐標。分別求兩個面的法向量,兩面垂直,則兩法向量也垂直,即數量積為0,從而可得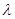 的值,若所得
的值,若所得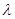 在
在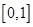 內說明存在點
內說明存在點 滿足條件,否則說明不存在。
滿足條件,否則說明不存在。
證明:(1)因為 為正四棱柱,
為正四棱柱,
所以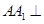 平面
平面 ,且
,且 為正方形. 1分
為正方形. 1分
因為 平面
平面 ,
,
所以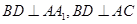 . 2分
. 2分
因為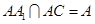 ,
,
所以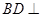 平面
平面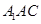 . 3分
. 3分
因為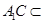 平面
平面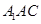 ,
,
所以 . 4分
. 4分
(2)如圖,以 為原點建立空間直角坐標系
為原點建立空間直角坐標系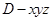 .則
.則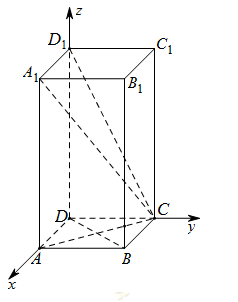
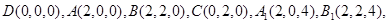
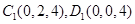 5分
5分
所以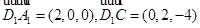 .
.
設平面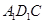 的法向量
的法向量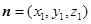 .
.
所以 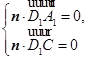 .即
.即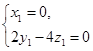 6分
6分
令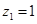 ,則
,則 .
.
所以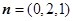 .
.
由(1)可知平面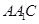 的法向量為
的法向量為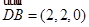 . 7分
. 7分
所以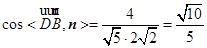 . 8分
. 8分
因為二面角 為鈍二面角,
為鈍二面角,
所以二面角 的余弦值為
的余弦值為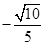 . 9分
. 9分
(3)設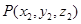 為線段
為線段


 全優點練單元計劃系列答案
全優點練單元計劃系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com