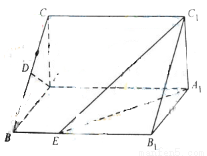
分析:(1)由韋達定理可得△ABC為等腰直角三角形,進而可得CD⊥AB,結合直棱柱的特征可得CD⊥AA1,結合線面垂直的判定定理可得CD⊥面A1ABB1,進而由線面垂直的定義可得DC⊥DE;
(2)由(1)可得CD⊥面A1ABB1,即CD為棱錐的高,求出三角形△A1DE的面積后,代入棱錐的體積公式,可得三棱錐C-A1DE的體積.
解答:證明:(1)由
AC=CB=AB,
AC
2+CB
2=AB
2故△ABC為等腰直角三角形
又由D是AB的中點,
知CD⊥AB,
又∵直棱柱ABC-A
1B
1C
1中,AA
1⊥平面ABC,CD?平面ABC,
∴CD⊥AA
1,
又∵AB,AA
1?面A
1ABB
1,AB∩AA
1=A
∴CD⊥面A
1ABB
1,
又∵DE?面A
1ABB
1,
故DC⊥DE;
(2)由(1)知CD⊥面A
1ABB
1,且CD=
在Rt△A
1AD中,AA
1=2,AD=
,
故A
1D=
在Rt△BDE中,BE=1,BD=
,
故DE=
Rt△A
1B
1E中,A
1B
1=2
,B
1E=1
故A
1E=3
∵
A1E2=A1D2+DE2故三角形△A
1DE為直角三角形
故
VC-A1DE=•CD••A1D•DE=••••=1.
點評:本題考查的知識點是線面垂直的判定定理及性質,棱錐的體積,其中證明出直線CD⊥面A1ABB1,是解答的關鍵.

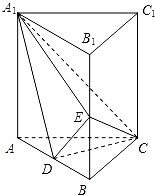 如圖,直棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點,AA1=AC=CB=
如圖,直棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點,AA1=AC=CB=

 如圖,直棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點,AA1=AC=CB=
如圖,直棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點,AA1=AC=CB=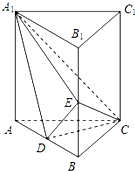 如圖,直棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點,AA1=AC=CB=
如圖,直棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點,AA1=AC=CB= 中,D,E分別是AB,BB1的中點,
中,D,E分別是AB,BB1的中點,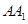 =AC=CB=
=AC=CB=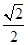 AB.
AB.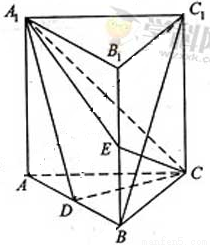
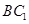 //平面
//平面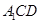 ;
;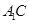 -E的正弦值.
-E的正弦值. ,AA1=3,D是BC的中點,點E在菱BB1上運動。
,AA1=3,D是BC的中點,點E在菱BB1上運動。