
| A. | xy=-1 | B. | xy=1 | C. | y2-x2=2 | D. | y2-x2=1 |
分析 設平面內曲線C上的點P(x,y),根據把點B繞點A逆時針方向旋轉θ角得到點P的定義,可求出其繞原點沿逆時針方向旋轉$\frac{π}{4}$后得到點P′($\frac{\sqrt{2}}{2}$(x-y),$\frac{\sqrt{2}}{2}$(x+y)),另由點P′在曲線x2-y2=2上,代入該方程即可求得原來曲線C的方程.
解答 解:設平面內曲線C上的點P(x,y),則其繞原點沿逆時針方向旋轉$\frac{π}{4}$后得到點P′($\frac{\sqrt{2}}{2}$(x-y),$\frac{\sqrt{2}}{2}$(x+y)),
∵點P′在曲線x2-y2=2上,
∴[$\frac{\sqrt{2}}{2}$(x-y)]2-[$\frac{\sqrt{2}}{2}$(x+y)]2=2,
整理得xy=-1.
故選:A.
點評 此題是基礎題.考查向量在幾何中的應用以及圓錐曲線的軌跡問題,同時考查學生的閱讀能力和分析解決問題的能力以及計算能力.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{2}$-$\frac{\sqrt{3}}{2}$i | B. | $\frac{3}{4}$-$\frac{\sqrt{3}}{4}$i | C. | $\frac{3}{2}$+$\frac{\sqrt{3}}{2}$i | D. | $\frac{3}{4}$+$\frac{\sqrt{3}}{4}$i |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
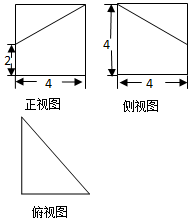
| A. | $\frac{32}{3}$ | B. | $\frac{50}{3}$ | C. | $\frac{64}{3}$ | D. | $\frac{80}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
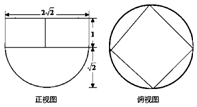
| A. | $2+\frac{{4\sqrt{2}π}}{3}$ | B. | $4+\frac{{8\sqrt{2}π}}{3}$ | C. | $2+\frac{{8\sqrt{2}π}}{3}$ | D. | $4+\frac{{4\sqrt{2}π}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
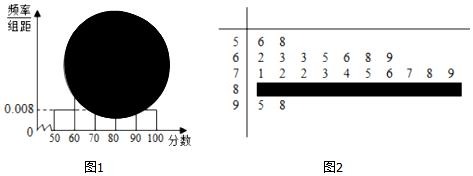
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com