【題目】已知函數
，那么下列結論中錯誤的是（ ）
A. 若
是
的極小值點，則在區間
上單調遞減
B. 
，使
C. 函數
的圖像可以是中心對稱圖形
D. 若是的極值點，則
【答案】A
【解析】分析：對于選項A，先求導得
，設其對應方程
的兩根為
。根據一元二次不等式的解法可得函數
的增區間為
，減區間為
，由此可得選項A說法錯誤；由選項A的解題過程可得選項B、D正確；對于選項C，取特殊值
，得特殊函數
，因為函數為奇函數，所以選項C正確。
詳解：對于選項A，，假設方程的兩根為。根據一元二次不等式的解法可得：由
得
或
，由
得
，所以函數的增區間為，減區間為，極小值點為
，所以選項A錯誤；
對于選項B，由選項A的解題過程可知在區間上，一定
，使
，所以選項B正確。
對于選項C，當時，函數，此函數圖像關于原點對稱。所以選項C正確；
對于選項D，由選項A的解題過程可知：若
是的極值點，則
。所以選項D正確。
故選A。
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】（1）已知sin(－π＋θ)＋2cos(3π－θ)=0，則
；
（2）已知
.
①化簡f(α)；
②若f(α)
，且
，求cos α－sin α的值；
③若
，求f(α)的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某射手每次射擊擊中目標的概率是
，且各次射擊的結果互不影響，假設這名射手射擊3次．
（1）求恰有2次擊中目標的概率；
（2）現在對射手的3次射擊進行計分：每擊中目標1次得1分，未擊中目標得0分；若僅有2次連續擊中，則額外加1分；若3次全擊中，則額外加3分．記
為射手射擊3次后的總得分，求的概率分布列與數學期望
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線C的參數方程是
（φ為參數，a>0），直線l的參數方程是
（t為參數），曲線C與直線l有一個公共點在x軸上，以坐標原點為極點，x軸的正半軸為極軸建立坐標系.
（1）求曲線C的普通方程；
（2）若點A（ρ1，θ），B（ρ2，θ＋
），C（ρ3，θ＋
）在曲線C上，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數
（其中
）的部分圖象如圖所示，把函數
的圖像向右平移
個單位長度，再向下平移1個單位，得到函數
的圖像.
（1）當
時，求的值域
（2）令
，若對任意
都有
恒成立，求
的最大值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖①，已知直角梯形ABCD中，
，
，過A作
，垂足為E.現將
沿AE折疊，使得
，如圖②.
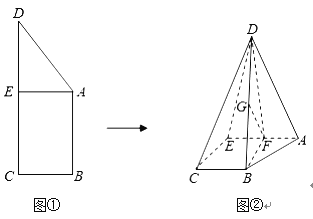
（1）求證：
；
（2）若FG分別為AE，DB的中點.
（i）求證：
平面DCE；
（ii）求證：平面
平面DBC.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在底面是菱形的四棱柱ABCD－A1B1C1D1中，∠ABC＝60°，AA1＝AC＝2，A1B＝A1D＝
，點E在A1D上
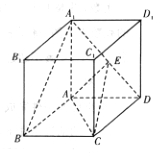
（1）求證：AA1⊥平面ABCD;
（2）當E為線段A1D的中點時，求點A1到平面EAC的距離
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
