【題目】某射手每次射擊擊中目標的概率是
，且各次射擊的結果互不影響，假設這名射手射擊3次．
（1）求恰有2次擊中目標的概率；
（2）現在對射手的3次射擊進行計分：每擊中目標1次得1分，未擊中目標得0分；若僅有2次連續擊中，則額外加1分；若3次全擊中，則額外加3分．記
為射手射擊3次后的總得分，求的概率分布列與數學期望
．
科目：高中數學 來源： 題型：
【題目】2012年12月18日，作為全國首批開展空氣質量新標準監測的74個城市之一，鄭州市正式發布
數據.資料表明，近幾年來，鄭州市霧霾治理取得了很大成效，空氣質量與前幾年相比得到了很大改善.鄭州市設有9個監測站點監測空氣質量指數（
），其中在輕度污染區、中度污染區、重度污染區分別設有2,5,2個監測站點，以9個站點測得的的平均值為依據，播報我市的空氣質量.
（Ⅰ）若某日播報的為118，已知輕度污染區的平均值為74，中度污染區的平均值為114，求重度污染區的平均值；
（Ⅱ）如圖是2018年11月的30天中的分布，11月份僅有一天在
內.
組數 | 分組 | 天數 |
第一組 |
| 3 |
第二組 |
| 4 |
第三組 |
| 4 |
第四組 |
| 6 |
第五組 |
| 5 |
第六組 |
| 4 |
第七組 |
| 3 |
第八組 |
| 1 |
①鄭州市某中學利用每周日的時間進行社會實踐活動，以公布的為標準，如果小于180，則去進行社會實踐活動.以統計數據中的頻率為概率，求該校周日進行社會實踐活動的概率；
②在“創建文明城市”活動中，驗收小組把鄭州市的空氣質量作為一個評價指標，從當月的空氣質量監測數據中抽取3天的數據進行評價，設抽取到不小于180的天數為
，求的分布列及數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
是由正整數組成的無窮數列，對任意
，
滿足如下兩個條件：①是
的倍數；②
.
（1）若
，
，寫出滿足條件的所有
的值；
（2）求證：當
時，
；
（3）求
所有可能取值中的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，已知點
是
軸與圓
的一個公共點（異于原點），拋物線
的準線為
，
上橫坐標為
的點
到的距離等于
.
（1）求的方程；
（2）直線
與圓
相切且與相交于
，
兩點，若
的面積為4，求的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖1所示，在
中， 
， 
， 
， 
為
的平分線，點
在線段
上， 
．如圖2所示，將
沿
折起，使得平面
平面
，連結
，設點
是
的中點．
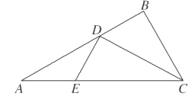
圖1 圖2
（1）求證： 
平面
；
（2）在圖2中，若
平面
，其中
為直線
與平面
的交點，求三棱錐
的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，那么下列結論中錯誤的是（ ）
A. 若
是
的極小值點，則在區間
上單調遞減
B. 
，使
C. 函數
的圖像可以是中心對稱圖形
D. 若是的極值點，則
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
外的有一點
，過點
作直線
.
（1）當直線
過圓心
時，求直線
的方程；
（2）當直線
與圓
相切時，求直線
的方程；
（3）當直線
的傾斜角為
時，求直線
被圓
所截得的弦長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
