
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
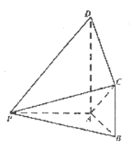
(1)求證:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析(2)![]()
【解析】
(1)因為![]() 所以要證
所以要證![]() 平面
平面![]() ,即證
,即證![]() 平面
平面![]() ,轉證
,轉證![]() (2)以點
(2)以點![]() 為坐標原點,
為坐標原點,![]() ,
,![]() ,
,![]() 分別為
分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸的正方向,建立如圖所示的空間直角坐標系
軸的正方向,建立如圖所示的空間直角坐標系![]() .分別求出平面
.分別求出平面![]() 與平面
與平面![]() 的法向量,代入公式,即可得到二面角
的法向量,代入公式,即可得到二面角![]() 的余弦值.
的余弦值.
(1)證明:取![]() 的中點
的中點![]() ,連接
,連接![]() ,所以
,所以![]() .
.
因為![]() ,所以四邊形
,所以四邊形![]() 為平行四邊形,
為平行四邊形,
所以![]() ,且
,且![]() .又
.又![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
又因為![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
又因為![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)由(1)知![]() 平面
平面![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,
,
故以點![]() 為坐標原點,
為坐標原點,![]() ,
,![]() ,
,![]() 分別為
分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸的正方向,
軸的正方向,
建立如圖所示的空間直角坐標系![]() .
.
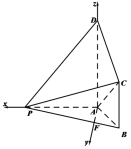
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
由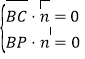 ,得
,得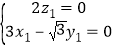 ,
,
取![]() ,得平面
,得平面![]() 的一個法向量為
的一個法向量為![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,
,
由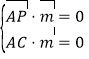 ,得
,得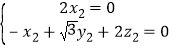 ,
,
取![]() ,得平面
,得平面![]() 的一個法向量為
的一個法向量為![]() ,
,
所以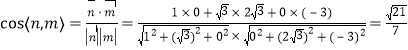 .
.
因為二面角![]() 是一個銳二面角,所以余弦值為
是一個銳二面角,所以余弦值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知點
中,已知點![]() 是
是![]() 軸與圓
軸與圓![]() 的一個公共點(異于原點),拋物線
的一個公共點(異于原點),拋物線![]() 的準線為
的準線為![]() ,
,![]() 上橫坐標為
上橫坐標為![]() 的點
的點![]() 到
到![]() 的距離等于
的距離等于![]() .
.
(1)求![]() 的方程;
的方程;
(2)直線![]() 與圓
與圓![]() 相切且與
相切且與![]() 相交于
相交于![]() ,
,![]() 兩點,若
兩點,若![]() 的面積為4,求
的面積為4,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,那么下列結論中錯誤的是( )
,那么下列結論中錯誤的是( )
A. 若![]() 是
是![]() 的極小值點,則
的極小值點,則![]() 在區間
在區間![]() 上單調遞減
上單調遞減
B. ![]() ,使
,使![]()
C. 函數![]() 的圖像可以是中心對稱圖形
的圖像可以是中心對稱圖形
D. 若![]() 是
是![]() 的極值點,則
的極值點,則![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(13分)設{an}是公比為正數的等比數列a1=2,a3=a2+4.
(Ⅰ)求{an}的通項公式;
(Ⅱ)設{bn}是首項為1,公差為2的等差數列,求數列{an+bn}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 外的有一點
外的有一點![]() ,過點
,過點![]() 作直線
作直線![]() .
.
(1)當直線![]() 過圓心
過圓心![]() 時,求直線
時,求直線![]() 的方程;
的方程;
(2)當直線![]() 與圓
與圓![]() 相切時,求直線
相切時,求直線![]() 的方程;
的方程;
(3)當直線![]() 的傾斜角為
的傾斜角為![]() 時,求直線
時,求直線![]() 被圓
被圓![]() 所截得的弦長.
所截得的弦長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是我國古代數學家趙爽在為《周髀算經》作注解時給出的“弦圖”.現提供4種顏色給“弦圖”的5個區域涂色,規定每個區域只涂一種顏色,相鄰區域顏色不相同,則不同的涂色方案共有( )
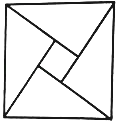
A.48種B.72種C.96種D.144種
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com