
【題目】已知函數![]() .
.
(![]() )當
)當![]() 時,求
時,求![]() 在區間
在區間![]() 上的取值范圍.
上的取值范圍.
(![]() )當
)當![]() 時,
時,![]() ,求
,求![]() 的值.
的值.
【答案】(1)當m=0時,![]()
![]() ,由已知
,由已知![]() ,得
,得![]()
從而得:![]() 的值域為
的值域為![]()
(2)![]()
化簡得:![]()
當![]() ,得:
,得:![]() ,
,![]() ,
,
代入上式,m=-2.
【解析】
試題(1)把m=0代入到f(x)中,然后分別利用同角三角函數間的基本關系、二倍角的正弦、余弦函數公式以及特殊角的三角函數值把f(x)化為一個角的正弦函數,利用x的范圍求出此正弦函數角的范圍,根據角的范圍,利用正弦函數的圖象即可得到f(x)的值域;
(2)把f(x)的解析式利用二倍角的正弦、余弦函數公式及積化和差公式化簡得到關于sin2x和cos2x的式子,把x換成α,根據tanα的值,利用同角三角函數間的基本關系以及二倍角的正弦函數公式化簡求出sin2α和cos2α的值,把sin2α和cos2α的值代入到f(α)=![]() 中得到關于m的方程,求出m的值即可.
中得到關于m的方程,求出m的值即可.
試題解析:(1)當m=0時,f(x)=(1+![]() )sin2x=sin2x+sinxcosx=
)sin2x=sin2x+sinxcosx=![]() ,由已知
,由已知![]() ,得
,得![]() ,從而得
,從而得![]() 的值域為[0,
的值域為[0,![]() ].
].
由f(x)=(1+![]() )sin2x+msin(x+
)sin2x+msin(x+![]() )sin(x-
)sin(x-![]() )
)
![]() ,所以
,所以![]() ,當
,當![]() ,得
,得![]() ,
,![]() ,代入式得
,代入式得![]()


科目:高中數學 來源: 題型:
【題目】如圖,在圓心角為![]() ,半徑為
,半徑為![]() 的扇形鐵皮上截取一塊矩形材料
的扇形鐵皮上截取一塊矩形材料![]() ,其中點
,其中點![]() 為圓心,點
為圓心,點![]() 在圓弧上,點
在圓弧上,點![]() 在兩半徑上,現將此矩形鐵皮
在兩半徑上,現將此矩形鐵皮![]() 卷成一個以
卷成一個以![]() 為母線的圓柱形鐵皮罐的側面(不計剪裁和拼接損耗),設矩形的邊長
為母線的圓柱形鐵皮罐的側面(不計剪裁和拼接損耗),設矩形的邊長![]() ,圓柱形鐵皮罐的容積為
,圓柱形鐵皮罐的容積為![]() .
.

(1)求圓柱形鐵皮罐的容積![]() 關于
關于![]() 的函數解析式,并指出該函數的定義域;
的函數解析式,并指出該函數的定義域;
(2)當![]() 為何值時,才使做出的圓柱形鐵皮罐的容積
為何值時,才使做出的圓柱形鐵皮罐的容積![]() 最大?最大容積是多少? (圓柱體積公式:
最大?最大容積是多少? (圓柱體積公式:![]() ,
,![]() 為圓柱的底面枳,
為圓柱的底面枳,![]() 為圓柱的高)
為圓柱的高)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.“sinα= ![]() ”是“cos2α=
”是“cos2α= ![]() ”的必要不充分條件
”的必要不充分條件
B.已知命題p:?x∈R,使2x>3x;命題q:?x∈(0,+∞),都有 ![]() <
< ![]() ,則p∧(¬q)是真命題
,則p∧(¬q)是真命題
C.命題“若xy=0,則x=0或y=0”的否命題是“若xy≠0,則x≠0或y≠0”
D.從勻速傳遞的生產流水線上,質檢員每隔5分鐘從中抽取一件產品進行某項指標檢測,這是分成抽樣
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)= ![]() sinxcosx+cos2x,銳角△ABC的三個角A,B,C所對的邊分別為a,b,c. (Ⅰ)求函數f(x)的最小正周期和單調遞增區間;
sinxcosx+cos2x,銳角△ABC的三個角A,B,C所對的邊分別為a,b,c. (Ⅰ)求函數f(x)的最小正周期和單調遞增區間;
(Ⅱ)若f(C)=1,求m= ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C是圓周上不同于A,B的任意一點,PA⊥平面ABC,則四面體P-ABC的四個面中,直角三角形的個數有( )
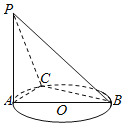
A. 4個B. 3個C. 2個D. 1個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,且滿足(2a-b)cosC-ccosB=0.
(Ⅰ)求角C的值;
(Ⅱ)若三邊a,b,c滿足a+b=13,c=7,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 一個焦點為
一個焦點為![]() ,離心率
,離心率![]() .
.
(Ⅰ)求橢圓![]() 的方程式.
的方程式.
(Ⅱ)定點![]() ,
,![]() 為橢圓
為橢圓![]() 上的動點,求
上的動點,求![]() 的最大值;并求出取最大值時
的最大值;并求出取最大值時![]() 點的坐標求.
點的坐標求.
(Ⅲ)定直線![]() ,
,![]() 為橢圓
為橢圓![]() 上的動點,證明點
上的動點,證明點![]() 到
到![]() 的距離與到定直線
的距離與到定直線![]() 的距離的比值為常數,并求出此常數值.
的距離的比值為常數,并求出此常數值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com