
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,直線
,直線![]() .
.
(1)若拋物線![]() 和直線
和直線![]() 沒有公共點,求
沒有公共點,求![]() 的取值范圍;
的取值范圍;
(2)若![]() ,且拋物線
,且拋物線![]() 和直線
和直線![]() 只有一個公共點
只有一個公共點![]() 時,求
時,求![]() 的值.
的值.
【答案】(1)![]() 或
或![]() ;(2)2.
;(2)2.
【解析】試題分析:(1)聯立方程![]() ,整理得
,整理得![]() ,
,
由拋物線![]() 和直線
和直線![]() 沒有公共點,則
沒有公共點,則![]() ,即可求得k的取值范圍;
,即可求得k的取值范圍;
(2)當拋物線![]() 和直線
和直線![]() 只有一個公共點時,記公共點坐標為
只有一個公共點時,記公共點坐標為![]() ,由
,由![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,因為
,因為![]() ,故
,故![]() ,將
,將![]() 代入
代入![]() 得
得![]() 求得x的值即得點M的坐標,可求
求得x的值即得點M的坐標,可求![]() 的值.
的值.
試題解析:(1)聯立方程![]() ,
,
整理得![]() ,
,
由拋物線![]() 和直線
和直線![]() 沒有公共點,則
沒有公共點,則![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() .
.
(2)當拋物線![]() 和直線
和直線![]() 只有一個公共點時,記公共點坐標為
只有一個公共點時,記公共點坐標為![]() ,
,
由![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
因為![]() ,故
,故![]() ,
,
將![]() 代入
代入![]() 得
得![]() ,解得
,解得![]() ,
,
由拋物線的定義知:![]() .
.
點睛:拋物線的定義是解決拋物線問題的基礎,它能將兩種距離(拋物線上的點到焦點的距離、拋物線上的點到準線的距離)進行等量轉化.如果問題中涉及拋物線的焦點和準線,又能與距離聯系起來,那么用拋物線定義就能解決問題.因此,涉及拋物線的焦半徑、焦點弦問題,可以優先考慮利用拋物線的定義轉化為點到準線的距離,這樣就可以使問題簡單化.


科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)若函數![]() 在
在![]() 處的切線平行于直線
處的切線平行于直線![]() ,求實數a的值;
,求實數a的值;
(Ⅱ)判斷函數![]() 在區間
在區間![]() 上零點的個數;
上零點的個數;
(Ⅲ)在(Ⅰ)的條件下,若在![]() 上存在一點
上存在一點![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,點
,點![]() 在橢圓C上,O為坐標原點.
在橢圓C上,O為坐標原點.
![]() Ⅰ
Ⅰ![]() 求橢圓C的方程;
求橢圓C的方程;
![]() Ⅱ
Ⅱ![]() 設動直線l與橢圓C有且僅有一個公共點,且l與圓
設動直線l與橢圓C有且僅有一個公共點,且l與圓![]() 的相交于不在坐標軸上的兩點
的相交于不在坐標軸上的兩點![]() ,
,![]() ,記直線
,記直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,求證:
,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對某產品1到6月份銷售量及其價格進行調查,其售價x和銷售量y之間的一組數據如下表所示:
月份i | 1 | 2 | 3 | 4 | 5 | 6 |
單價 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
銷售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根據1至5月份的數據,求出y關于x的回歸直線方程;
(2)若由回歸直線方程得到的估計數據與剩下的檢驗數據的誤差不超過0.5元,則認為所得到的回歸直線方程是理想的,試問所得到的回歸直線方程是否理想?
(3)預計在今后的銷售中,銷售量與單價仍然服從(1)中的關系,且該產品的成本是2.5元/件,為獲得最大利潤,該產品的單價應定為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“大眾創業,萬眾創新”是李克強總理在本屆政府工作報告中向全國人民發出的口號.某生產企業積極響應號召,大力研發新產品,為了對新研發的一批產品進行合理定價,將該產品按事先擬定的價格進行試銷,得到一組銷售數據![]() ,如表所示:
,如表所示:
試銷單價x(元) | 4 | 5 | 6 | 7 | 8 |
產品銷量y(件) | q | 85 | 82 | 80 | 75 |
已知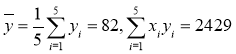
(1)求出q的值;
(2)已知變量![]() 具有線性相關關系,求產品銷量y(件)關于試銷單價x(元)的線性回歸方程
具有線性相關關系,求產品銷量y(件)關于試銷單價x(元)的線性回歸方程![]() ;
;
(3)假設試銷單價為10元,試估計該產品的銷量.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]()
(1)若“![]() x∈A,使得x∈B”為真命題,求m的取值范圍;
x∈A,使得x∈B”為真命題,求m的取值范圍;
(2)是否存在實數m,使“x∈A”是“X∈B”必要不充分條件,若存在,求出m的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經調查統計,網民在網上光顧某淘寶小店,經過一番瀏覽后,對該店鋪中的![]() 三種商品有購買意向.該淘寶小店推出買一種送5元優惠券的活動.已知某網民購買
三種商品有購買意向.該淘寶小店推出買一種送5元優惠券的活動.已知某網民購買![]() 商品的概率分別為
商品的概率分別為![]() ,
,![]() ,
,![]() ,至少購買一種的概率為
,至少購買一種的概率為![]() ,最多購買兩種的概率為
,最多購買兩種的概率為![]() .假設該網民是否購買這三種商品相互獨立.
.假設該網民是否購買這三種商品相互獨立.
(1)求該網民分別購買![]() 兩種商品的概率;
兩種商品的概率;
(2)用隨機變量![]() 表示該網民購買商品所享受的優惠券錢數,求
表示該網民購買商品所享受的優惠券錢數,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】孝感市旅游局為了了解雙峰山景點在大眾中的熟知度,從年齡在15~65歲的人群中隨機抽取![]() 人進行問卷調查,把這
人進行問卷調查,把這![]() 人按年齡分成5組:第一組
人按年齡分成5組:第一組![]() ,第二組
,第二組![]() ,第三組
,第三組![]() ,第四組
,第四組![]() ,第五組
,第五組![]() ,得到的樣本的頻率分布直方圖如圖:
,得到的樣本的頻率分布直方圖如圖:
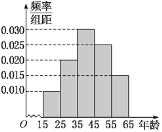
調查問題是“雙峰山國家森林公園是幾![]() 級旅游景點?”每組中回答正確的人數及回答正確的人數占本組的頻率的統計結果如下表.
級旅游景點?”每組中回答正確的人數及回答正確的人數占本組的頻率的統計結果如下表.
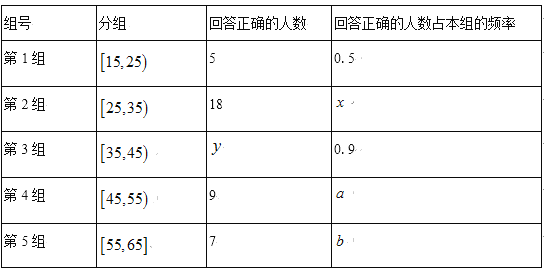
(1)分別求出![]() 的值;
的值;
(2)從第2,3,4組回答正確的人中用分層抽樣的方法抽取6人,求第2,3,4組每組各抽取多少人;
(3)在(2)抽取的6人中隨機抽取2人,求所抽取的兩人來自不同年齡組的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com