
(本小題滿分12分)
已知函數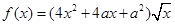 ,其中
,其中 .
.
(1)當 時,求
時,求 的單調遞增區間;
的單調遞增區間;
(2)若 在區間
在區間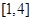 上的最小值為8,求
上的最小值為8,求 的值.
的值.
(1)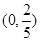 和
和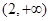 ,(2)
,(2)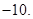
解析試題分析:(1)利用導數求函數單調區間,首先確定定義域: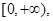 然后對函數求導,在定義域內求導函數的零點:
然后對函數求導,在定義域內求導函數的零點: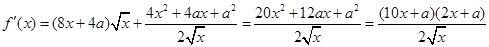 ,當
,當 時,
時,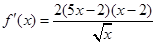 ,由
,由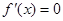 得
得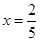 或
或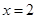 ,列表分析得單調增區間:
,列表分析得單調增區間: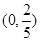 和
和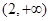 ,(2)已知函數最值,求參數,解題思路還是從求最值出發.由(1)知,
,(2)已知函數最值,求參數,解題思路還是從求最值出發.由(1)知,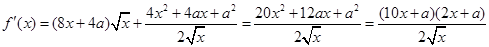 ,所以導函數的零點為
,所以導函數的零點為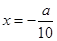 或
或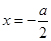 ,列表分析可得:函數增區間為
,列表分析可得:函數增區間為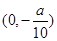 和
和 ,減區間為
,減區間為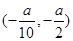 .由于
.由于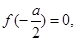 所以
所以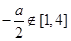 ,當
,當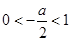 時,
時,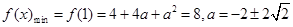 ,(舍),當
,(舍),當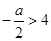 時,
時,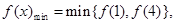 由于
由于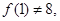 所以
所以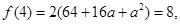 且
且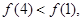 解得
解得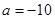 或
或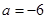 (舍),當
(舍),當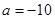 時,
時, 在
在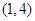 上單調遞減,滿足題意,綜上
上單調遞減,滿足題意,綜上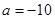 .
.
試題解析:(1)定義域: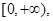 而
而 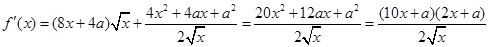 ,當
,當 時,
時,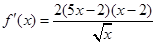 ,由
,由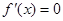 得
得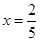 或
或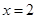 ,列表:
,列表: