【題目】關(guān)于
的方程
的實根個數(shù)記
.（1）若
，則=____________；（2）若
，存在
使得
成立，則
的取值范圍是_____.
【答案】
【解析】
（1）根據(jù)一次函數(shù)的特點(diǎn)直接可得到此時
的值；
（2）利用函數(shù)圖象先考慮
是否滿足，再利用圖象分析
時
滿足要求時對應(yīng)的不等式，從而求解出
的取值范圍.
（1）若g（x）=x+1，則函數(shù)的值域為R，且函數(shù)為單調(diào)函數(shù)，故方程g（x）=t有且只有一個根，故f（t）=1，
（2）
當(dāng)時，利用圖象分析可知：
如下圖，此時
，
，不滿足題意；
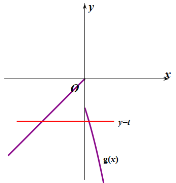
如下圖，此時
，，不滿足題意；
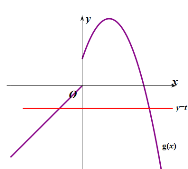
當(dāng)時，利用圖象分析可知：
當(dāng)時，由上面圖象分析可知不符合題意，
當(dāng)時，若要滿足
，如下圖所示：
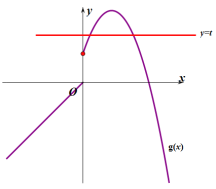
只需滿足：，
，所以
，解得
.
綜上可知：
.
故答案為：；.
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知集合A＝{x|x2－2x－3≤0}，B＝{x|x2－2mx＋m2－4≤0，x∈R，m∈R}．
(1)若A∩B＝[0,3]，求實數(shù)m的值；
(2)若ARB，求實數(shù)m的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
．
（Ⅰ）求函數(shù)
的單調(diào)遞增區(qū)間；
（Ⅱ）若對任意的實數(shù)
，都有
成立，求實數(shù)
的取值范圍；
（Ⅲ）若
，
的最大值是
，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
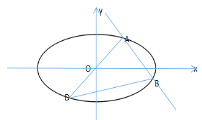
【題目】已知橢圓
的中心在原點(diǎn)，焦點(diǎn)在
軸上，短軸長和焦距都等于2，
是橢圓上的一點(diǎn)，且在第一象限內(nèi)，過且斜率等于
的直線與橢圓交于另一點(diǎn)
，點(diǎn)關(guān)于原點(diǎn)的對稱點(diǎn)為
.
（1）求橢圓的方程；
（2）證明：直線
的斜率為定值；
（3）求
面積的最大值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
長軸是短軸的
倍，且右焦點(diǎn)為
.
（Ⅰ）求橢圓C的標(biāo)準(zhǔn)方程；
（Ⅱ）直線
交橢圓
于
兩點(diǎn)，若線段
中點(diǎn)的橫坐標(biāo)為
，求直線
的方程及
的面積.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】命題
：指數(shù)函數(shù)
是減函數(shù)；命題
：
，使關(guān)于
的方程
有實數(shù)解，其中
.
(1)當(dāng)
時，若為真命題，求
的取值范圍；
(2)當(dāng)
時，若且為假命題，求的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
（
，且
為自然對數(shù)的底數(shù)）
（1）判斷函數(shù)
的單調(diào)性并證明；
（2）判斷函數(shù)的奇偶性并證明；
（3）是否存在實數(shù)
，使不等式
對一切
都成立？若存在，求出的范圍，若不存在說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】古希臘時期，人們認(rèn)為最美人體的頭頂至肚臍的長度與肚臍至足底的長度之比是
（≈0.618，稱為黃金分割比例)，著名的“斷臂維納斯”便是如此．此外，最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是．若某人滿足上述兩個黃金分割比例，且腿長為105cm，頭頂至脖子下端的長度為26 cm，則其身高可能是
A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
