
【題目】已知a>0且a≠1,函數f(x)=loga(x+1), ![]() ,記F(x)=2f(x)+g(x)
,記F(x)=2f(x)+g(x)
(1)求函數F(x)的定義域D及其零點;
(2)試討論函數F(x)在定義域D上的單調性;
(3)若關于x的方程F(x)﹣2m2+3m+5=0在區間[0,1)內僅有一解,求實數m的取值范圍.
【答案】
(1)解:F(x)=2f(x)+g(x)= ![]() (a>0且a≠1)
(a>0且a≠1)
要使函數有意義,則 ![]() ,解得﹣1<x<1,
,解得﹣1<x<1,
∴函數F(x)的定義域為(﹣1,1).
令F(x)=0,則 ![]() …(*)
…(*)
方程變為 ![]() ,(x+1)2=1﹣x,即x2+3x=0
,(x+1)2=1﹣x,即x2+3x=0
解得x1=0,x2=﹣3.
經檢驗x=﹣3是(*)的增根,∴方程(*)的解為x=0,
∴函數F(x)的零點為0
(2)解:由于函數 ![]() 在定義域D上是增函數.可得:
在定義域D上是增函數.可得:
①當a>1時,由復合函數的單調性知:函數f(x)=loga(x+1), ![]()
在定義域D上是增函數.
∴函數F(x)=2f(x)+g(x)在定義域D上是增函數.
②當0<a<1時,由復合函數的單調性知:
函數f(x)=loga(x+1), ![]() ,在定義域D上是減函數.
,在定義域D上是減函數.
∴函數F(x)=2f(x)+g(x)在定義域D上是減函數
(3)解:問題等價于關于x的方程2m2﹣3m﹣5=F(x)在區間[0,1)內僅有一解,
①當a>1時,由(2)知,函數F(x)在[0,1)上是增函數,
∴F(x)∈[0,+∞),
∴只需2m2﹣3m﹣5≥0,
解得:m≤﹣1,或 ![]() .
.
②當0<a<1時,由(2)知,函數F(x)在[0,1)上是減函數,
∴F(x)∈(﹣∞,0],
∴只需2m2﹣3m﹣5≤0,
解得: ![]() .
.
綜上所述,當0<a<1時: ![]() ;
;
當a>1時,m≤﹣1,或 ![]()
【解析】(1)利用對數函數的定義域即可的得出,利用對數的運算法則即可得出函數的零點;(2)通過對a分類討論,利用一次函數、反比例函數、對數函數的單調性即可得出復合函數F(x)的單調性;(3)利用(2)的函數F(x)的單調性可得其值域,進而轉化為即一元二次不等式的解集.
【考點精析】掌握函數的定義域及其求法和函數單調性的判斷方法是解答本題的根本,需要知道求函數的定義域時,一般遵循以下原則:①![]() 是整式時,定義域是全體實數;②
是整式時,定義域是全體實數;②![]() 是分式函數時,定義域是使分母不為零的一切實數;③
是分式函數時,定義域是使分母不為零的一切實數;③![]() 是偶次根式時,定義域是使被開方式為非負值時的實數的集合;④對數函數的真數大于零,當對數或指數函數的底數中含變量時,底數須大于零且不等于1,零(負)指數冪的底數不能為零;單調性的判定法:①設x1,x2是所研究區間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較.
是偶次根式時,定義域是使被開方式為非負值時的實數的集合;④對數函數的真數大于零,當對數或指數函數的底數中含變量時,底數須大于零且不等于1,零(負)指數冪的底數不能為零;單調性的判定法:①設x1,x2是所研究區間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較.


科目:高中數學 來源: 題型:
【題目】己知f(x)=x2﹣2x+2,在[ ![]() ,m2﹣m+2]上任取三個數a,b,c,均存在以 f(a),f(b),f(c)為三邊的三角形,則m的取值范圍為( )
,m2﹣m+2]上任取三個數a,b,c,均存在以 f(a),f(b),f(c)為三邊的三角形,則m的取值范圍為( )
A.(0,1)
B.[0, ![]() )
)
C.(0, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩名同學在5次英語口語測試中的成績統計如圖的莖葉圖所示.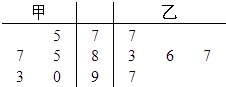
(注:樣本數據x1 , x2 , …,xn的方差s2= ![]() [
[ ![]() +
+ ![]() +…+
+…+ ![]() ],其中
],其中 ![]() 表示樣本均值)
表示樣本均值)
(1)現要從中選派一人參加英語口語競賽,從兩同學的平均成績和方差分析,派誰參加更合適;
(2)若將頻率視為概率,對學生甲在今后的三次英語口語競賽成績進行預測,記這三次成績中高于80分的次數為ξ,求ξ的分布列及數學期望Eξ.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的上下兩個焦點分別為
的上下兩個焦點分別為![]() ,
, ![]() ,過點
,過點![]() 與
與![]() 軸垂直的直線交橢圓
軸垂直的直線交橢圓![]() 于
于![]() 、
、![]() 兩點,
兩點, ![]() 的面積為
的面積為![]() ,橢圓
,橢圓![]() 的離心力為
的離心力為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)已知![]() 為坐標原點,直線
為坐標原點,直線![]() :
: ![]() 與
與![]() 軸交于點
軸交于點![]() ,與橢圓
,與橢圓![]() 交于
交于![]() ,
, ![]() 兩個不同的點,若存在實數
兩個不同的點,若存在實數![]() ,使得
,使得![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中正確的有( )
①冪函數的圖象一定不過第四象限;
②已知常數a>0且a≠1,則函數f(x)=ax﹣1﹣1恒過定點(1,0);
③若存在x1 , x2∈I,當x1<x2時,f(x1)<f(x2),則y=f(x)在I上是增函數;
④ ![]() 的單調減區間是(﹣∞,0)∪(0,+∞).
的單調減區間是(﹣∞,0)∪(0,+∞).
A.0個
B.1個
C.2個
D.3個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校高三年級有學生500人,其中男生300人,女生200人,為了研究學生的數學成績是否與性別有關,現采用分層抽樣的方法,從中抽取了100名學生,先統計了他們期中考試的數學分數,然后按性別分為男、女兩組,再將兩組學生的分數分成5組:[100,110),[110,120),[120,130),[130,140),[140,150]分別加以統計,得到如圖所示的頻率分布直方圖.
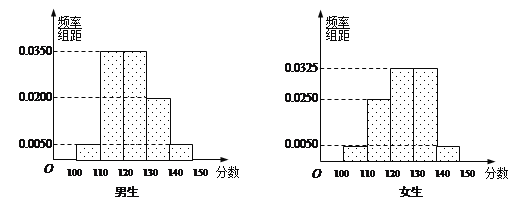
(1)從樣本中分數小于110分的學生中隨機抽取2人,求兩人恰好為一男一女的概率;
(2)若規定分數不小于130分的學生為“數學尖子生”,請你根據已知條件完成2×2列聯表,并判斷是否有90%的把握認為“數學尖子生與性別有關”?
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
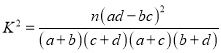 ,
,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}中,a1= ![]() ,an=
,an= ![]() (n≥2,n∈N+).
(n≥2,n∈N+).
(1)求a2 , a3 , a4的值,并猜想數列{an}的通項公式an .
(2)用數學歸納法證明你猜想的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com