
【題目】設函數![]()
![]() .
.
(1)求函數![]() 的最小值;
的最小值;
(2)設![]() ,討論函數
,討論函數![]() 的單調性;
的單調性;
(3)斜率為![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() 、
、![]()
![]() 兩點,
兩點,
求證:![]()
【答案】(1)![]() ;(2)當
;(2)當![]() 時,
時,![]() 在
在![]() 上是增函數;當
上是增函數;當![]() 時,
時,![]() 在
在![]() 上單調遞增,在
上單調遞增,在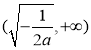 上單調遞減;(3)見解析.
上單調遞減;(3)見解析.
【解析】
(1)對函數![]() 求導,求其單調區間,即可求出極值,可得最小值;(2)分別討論
求導,求其單調區間,即可求出極值,可得最小值;(2)分別討論![]() 和
和![]() 時函數
時函數![]() 的單調性;(3)將直線斜率
的單調性;(3)將直線斜率![]() 用
用![]() 表示出來,將要證的不等式轉化為證
表示出來,將要證的不等式轉化為證![]() (
(![]() ),最后討論函數
),最后討論函數![]() (
(![]() )和
)和![]() (
(![]() )單調性,即可證明原題.
)單調性,即可證明原題.
(1)![]() ,令
,令![]() ,得
,得![]()
因為當![]() 時
時![]() ;當
;當![]() 時
時![]() ,
,
所以當![]() 時,
時,![]()
(2)![]() ,
,![]()
①當![]() 時,恒有
時,恒有![]() ,
,![]() 在
在![]() 上是增函數;
上是增函數;
②當![]() 時,
時,
令![]() ,得
,得![]() ,解得
,解得![]() ;
;
令![]() ,得
,得![]() ,解得
,解得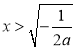 ,
,
綜上,當![]() 時,
時,![]() 在
在![]() 上是增函數;
上是增函數;
當![]() 時,
時,![]() 在
在![]() 上單調遞增,在
上單調遞增,在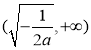 上單調遞減
上單調遞減
(3) ![]() .
.
要證![]() ,即證
,即證![]() ,等價于證
,等價于證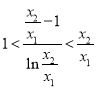 ,令
,令![]() ,
,
則只要證![]() ,由
,由![]() 知
知![]() ,故等價于證
,故等價于證![]() (*).
(*).
① 設![]() ,則
,則![]() ,故
,故![]() 在
在![]() 上是增函數,
上是增函數,
∴ 當![]() 時,
時,![]() ,即
,即![]() .
.
② 設![]() ,則
,則![]() ,故
,故![]() 在
在![]() 上是增函數,
上是增函數,
∴ 當![]() 時,
時,![]() ,即
,即![]() .
.
由①②知(*)成立,![]() 得證.
得證.


科目:高中數學 來源: 題型:
【題目】類比平面幾何中的定理:△ABC中,若DE是△ABC的中位線,則有S△ADE∶S△ABC=1∶4;若三棱錐A-BCD有中截面EFG∥平面BCD,則截得三棱錐的體積與原三棱錐體積之間的關系式為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為區間
的定義域為區間![]() ,若對于
,若對于![]() 內任意
內任意![]() ,都有
,都有![]()
![]() 成立,則稱函數
成立,則稱函數![]() 是區間
是區間![]() 的“
的“![]() 函數”.
函數”.
(1)判斷函數![]() (
(![]() )是否是“
)是否是“![]() 函數”?說明理由;
函數”?說明理由;
(2)已知![]() ,求證:函數
,求證:函數![]() (
(![]() )是“
)是“![]() 函數”;
函數”;
(3)設函數![]() 是
是![]() ,(
,(![]() )上的“
)上的“![]() 函數”,
函數”,![]() ,且存在
,且存在![]() 使得
使得![]() ,試探討函數
,試探討函數![]() 在區間
在區間![]() 上零點個數,并用圖象作出簡要的說明(結果不需要證明).
上零點個數,并用圖象作出簡要的說明(結果不需要證明).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一臺機器使用的時間較長,但還可以使用,它按不同的轉速生產出來的某機械零件有一些會有缺點,每小時生產有缺點零件的多少,隨機器的運轉的速度而變化,下表為抽樣試驗的結果:
轉速x(轉/秒) | 2 | 4 | 5 | 6 | 8 |
每小時生產有缺點的零件數y(件) | 30 | 40 | 60 | 50 | 70 |
(1)畫散點圖;
(2)如果y對x有線性相關關系,求回歸直線方程;
(3)若實際生產中,允許每小時的產品中有缺點的零件最多為89個,那么機器的運轉速度應控制在什么范圍內?(參考數值:![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+2﹣alnx﹣bx(a>0).
(Ⅰ)若a=1,b=3,求函數y=f(x)在(1,f(1))處的切線方程;
(Ⅱ)若f(x1)=f(x2)=0,且x1≠x2,證明:f′(![]() )>0.
)>0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列關于回歸分析的說法中錯誤的是( )
A. 回歸直線一定過樣本中心![]()
B. 殘差圖中殘差點比較均勻地落在水平的帶狀區域中,說明選用的模型比較合適
C. 兩個模型中殘差平方和越小的模型擬合的效果越好
D. 甲、乙兩個模型的![]() 分別約為0.98和0.80,則模型乙的擬合效果更好
分別約為0.98和0.80,則模型乙的擬合效果更好
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com