
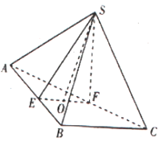
 如圖,三棱錐S-ABC,E,F分別在線段AB,AC上,EF∥BC,△ABC,△SEF均是等邊三角形,且平面SEF⊥平面ABC,若BC=4,EF=a,O為EF的中點.
如圖,三棱錐S-ABC,E,F分別在線段AB,AC上,EF∥BC,△ABC,△SEF均是等邊三角形,且平面SEF⊥平面ABC,若BC=4,EF=a,O為EF的中點.分析 (1)利用平面SEF⊥平面ABC,得出SO⊥平面ABC,BC⊥SO,
再由等邊△ABC中AO⊥BC,得出BC⊥平面AOS,從而證明BC⊥AS;
(2)由SO⊥平面ABC得SO⊥BE,要使BE⊥平面SCD,則需BE⊥CO,
利用AE=EF求出a的值,得出此時BE⊥平面SCO.
解答 解:(1)證明:因為平面SEF⊥平面ABC,O為EF的中點,
且SE=SF,
∴SO⊥EF,
∴SO⊥平面ABC,
又BC?平面ABC,BC⊥SO,
而在等邊△ABC中,AO⊥BC,
且SO∩AO=O,
∴BC⊥平面AOS,
又AS?平面AOS,∴BC⊥AS;
(2)平面SEF⊥平面ABC,O為EF的中點,且SE=SF,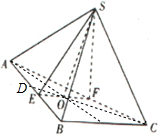
∴SO⊥平面ABC,故SO⊥BE,
要使BE⊥平面SCD,則需BE⊥CO,
延長CO交AB于D,則CD⊥AB,
DE=$\frac{1}{2}$EO=$\frac{1}{4}$a,
AD=2,
∴AE=2+$\frac{1}{4}$a,
即AE=EF
2+$\frac{1}{4}$a=a,
解得a=$\frac{8}{3}$;
∴a=$\frac{8}{3}$時,BE⊥平面SCO.
點評 本題考查了空間中的垂直關系的應用問題,是綜合性題目.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {1,2,3,4} | B. | {1,3,4} | C. | {1,2,3,8,4,7} | D. | {0,1,2,3,4,7,8} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
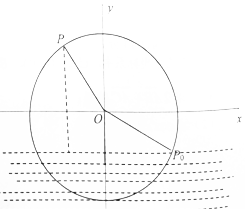 一半徑為4米的水輪如圖所示,水輪圓心O距離水面2米,已知水輪每60秒逆時針轉動5圈,如果當水輪上點P從水中浮現時(圖象P0點)開始計算時間,且點P距離水面的高度f(t)(米)與時間t(秒)滿足函數:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).
一半徑為4米的水輪如圖所示,水輪圓心O距離水面2米,已知水輪每60秒逆時針轉動5圈,如果當水輪上點P從水中浮現時(圖象P0點)開始計算時間,且點P距離水面的高度f(t)(米)與時間t(秒)滿足函數:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com