
【題目】已知函數(shù)![]() ,函數(shù)
,函數(shù)![]() 在點
在點![]() 處的切線斜率為0.
處的切線斜率為0.
(1)試用含有![]() 的式子表示
的式子表示![]() ,并討論
,并討論![]() 的單調(diào)性;
的單調(diào)性;
(2)對于函數(shù)![]() 圖象上的不同兩點
圖象上的不同兩點![]() ,
,![]() ,如果在函數(shù)
,如果在函數(shù)![]() 圖象上存在點
圖象上存在點![]() ,使得在點
,使得在點![]() 處的切線
處的切線![]() ,則稱
,則稱![]() 存在“跟隨切線”.特別地,當
存在“跟隨切線”.特別地,當![]() 時,又稱
時,又稱![]() 存在“中值跟隨切線”.試問:函數(shù)
存在“中值跟隨切線”.試問:函數(shù)![]() 上是否存在兩點
上是否存在兩點![]() 使得它存在“中值跟隨切線”,若存在,求出
使得它存在“中值跟隨切線”,若存在,求出![]() 的坐標,若不存在,說明理由.
的坐標,若不存在,說明理由.
【答案】(1)![]() ,單調(diào)性見解析;(2)不存在,理由見解析
,單調(diào)性見解析;(2)不存在,理由見解析
【解析】
(1)由題意得![]() ,即可得
,即可得![]() ;求出函數(shù)
;求出函數(shù)![]() 的導數(shù)
的導數(shù)![]() ,再根據(jù)
,再根據(jù)![]() 、
、![]() 、
、![]() 、
、![]() 分類討論,分別求出
分類討論,分別求出![]() 、
、![]() 的解集即可得解;
的解集即可得解;
(2)假設滿足條件的![]() 、
、![]() 存在,不妨設
存在,不妨設![]() ,
,![]() 且
且![]() ,由題意得
,由題意得![]() 可得
可得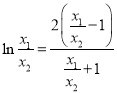 ,令
,令![]() (
(![]() ),構(gòu)造函數(shù)
),構(gòu)造函數(shù)![]() (
(![]() ),求導后證明
),求導后證明![]() 即可得解.
即可得解.
(1)由題可得函數(shù)![]() 的定義域為
的定義域為![]() 且
且![]() ,
,
由![]() ,整理得
,整理得![]() .
.
![]() .
.
(ⅰ)當![]() 時,易知
時,易知![]() ,
,![]() ,
,![]() 時
時![]() .
.
故![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減.
上單調(diào)遞減.
(ⅱ)當![]() 時,令
時,令![]() ,解得
,解得![]() 或
或![]() ,則
,則
①當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上恒成立,則
上恒成立,則![]() 在
在![]() 上遞增.
上遞增.
②當![]() ,即
,即![]() 時,當
時,當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() .
.
所以![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,![]() 單調(diào)遞減,
單調(diào)遞減,![]() 單調(diào)遞增.
單調(diào)遞增.
③當![]() ,即
,即![]() 時,當
時,當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
所以![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,![]() 單調(diào)遞減,
單調(diào)遞減,![]() 單調(diào)遞增.
單調(diào)遞增.
綜上,當![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 單調(diào)遞減.
單調(diào)遞減.
當![]() 時,
時,![]() 在
在![]() 及
及![]() 上單調(diào)遞增;
上單調(diào)遞增;![]() 在
在![]() 上單調(diào)遞減.
上單調(diào)遞減.
當![]() 時,
時,![]() 在
在![]() 上遞增.
上遞增.
當![]() 時,
時,![]() 在
在![]() 及
及![]() 上單調(diào)遞增;
上單調(diào)遞增;![]() 在
在![]() 上遞減.
上遞減.
(2)滿足條件的![]() 、
、![]() 不存在,理由如下:
不存在,理由如下:
假設滿足條件的![]() 、
、![]() 存在,不妨設
存在,不妨設![]() ,
,![]() 且
且![]() ,
,
則![]() ,
,
又![]() ,
,
由題可知![]() ,整理可得:
,整理可得: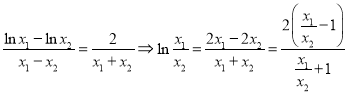 ,
,
令![]() (
(![]() ),構(gòu)造函數(shù)
),構(gòu)造函數(shù)![]() (
(![]() ).
).
則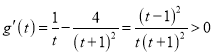 ,
,
所以![]() 在
在![]() 上單調(diào)遞增,從而
上單調(diào)遞增,從而![]() ,
,
所以方程![]() 無解,即
無解,即![]() 無解.
無解.
綜上,滿足條件的A、B不存在.


科目:高中數(shù)學 來源: 題型:
【題目】超級病菌是一種耐藥性細菌,產(chǎn)生超級細菌的主要原因是用于抵抗細菌侵蝕的藥物越來越多,但是由于濫用抗生素的現(xiàn)象不斷的發(fā)生,很多致病菌也對相應的抗生素產(chǎn)生了耐藥性,更可怕的是,抗生素藥物對它起不到什么作用,病人會因為感染而引起可怕的炎癥,高燒、痙攣、昏迷直到最后死亡.某藥物研究所為篩查某種超級細菌,需要檢驗血液是否為陽性,現(xiàn)有n(![]() )份血液樣本,每個樣本取到的可能性均等,有以下兩種檢驗方式:
)份血液樣本,每個樣本取到的可能性均等,有以下兩種檢驗方式:
(1)逐份檢驗,則需要檢驗n次;
(2)混合檢驗,將其中k(![]() 且
且![]() )份血液樣本分別取樣混合在一起檢驗,若檢驗結(jié)果為陰性,這k份的血液全為陰性,因而這k份血液樣本只要檢驗一次就夠了,如果檢驗結(jié)果為陽性,為了明確這k份血液究竟哪幾份為陽性,就要對這k份再逐份檢驗,此時這k份血液的檢驗次數(shù)總共為
)份血液樣本分別取樣混合在一起檢驗,若檢驗結(jié)果為陰性,這k份的血液全為陰性,因而這k份血液樣本只要檢驗一次就夠了,如果檢驗結(jié)果為陽性,為了明確這k份血液究竟哪幾份為陽性,就要對這k份再逐份檢驗,此時這k份血液的檢驗次數(shù)總共為![]() 次,假設在接受檢驗的血液樣本中,每份樣本的檢驗結(jié)果是陽性還是陰性都是獨立的,且每份樣本是陽性結(jié)果的概率為p(
次,假設在接受檢驗的血液樣本中,每份樣本的檢驗結(jié)果是陽性還是陰性都是獨立的,且每份樣本是陽性結(jié)果的概率為p(![]() ).
).
(1)假設有5份血液樣本,其中只有2份樣本為陽性,若采用逐份檢驗方式,求恰好經(jīng)過2次檢驗就能把陽性樣本全部檢驗出來的概率;
(2)現(xiàn)取其中k(![]() 且
且![]() )份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的總次數(shù)為
)份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的總次數(shù)為![]() ,采用混合檢驗方式,樣本需要檢驗的總次數(shù)為
,采用混合檢驗方式,樣本需要檢驗的總次數(shù)為![]() .
.
(i)試運用概率統(tǒng)計的知識,若![]() ,試求p關(guān)于k的函數(shù)關(guān)系式
,試求p關(guān)于k的函數(shù)關(guān)系式![]() ;
;
(ii)若![]() ,采用混合檢驗方式可以使得樣本需要檢驗的總次數(shù)的期望值比逐份檢驗的總次數(shù)期望值更少,求k的最大值.
,采用混合檢驗方式可以使得樣本需要檢驗的總次數(shù)的期望值比逐份檢驗的總次數(shù)期望值更少,求k的最大值.
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=aex,g(x)=lnx-lna,其中a為常數(shù),且曲線y=f(x)在其與y軸的交點處的切線記為l1,曲線y=g(x)在其與x軸的交點處的切線記為l2,且l1∥l2.
(1)求l1,l2之間的距離;
(2)若存在x使不等式![]() 成立,求實數(shù)m的取值范圍;
成立,求實數(shù)m的取值范圍;
(3)對于函數(shù)f(x)和g(x)的公共定義域中的任意實數(shù)x0,稱|f(x0)-g(x0)|的值為兩函數(shù)在x0處的偏差.求證:函數(shù)f(x)和g(x)在其公共定義域內(nèi)的所有偏差都大于2.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】我國南宋數(shù)學家楊輝所著的《詳解九章算術(shù)》一書中,用圖①的數(shù)表列出了一些正整數(shù)在三角形中的一種幾何排列,俗稱“楊輝三角形”,該數(shù)表的規(guī)律是每行首尾數(shù)字均為![]() ,從第三行開始,其余的數(shù)字是它“上方”左右兩個數(shù)字之和。現(xiàn)將楊輝三角形中的奇數(shù)換成
,從第三行開始,其余的數(shù)字是它“上方”左右兩個數(shù)字之和。現(xiàn)將楊輝三角形中的奇數(shù)換成![]() ,偶數(shù)換成
,偶數(shù)換成![]() ,得到圖②所示的由數(shù)字
,得到圖②所示的由數(shù)字![]() 和
和![]() 組成的三角形數(shù)表,由上往下數(shù),記第
組成的三角形數(shù)表,由上往下數(shù),記第![]() 行各數(shù)字的和為
行各數(shù)字的和為![]() ,如
,如![]() ,則
,則![]() ____________
____________
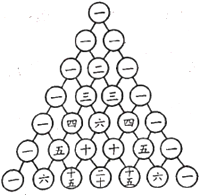

① ②
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】 設橢圓![]() 的左焦點為
的左焦點為![]() ,左頂點為
,左頂點為![]() ,頂點為B.已知
,頂點為B.已知![]() (
(![]() 為原點).
為原點).
(Ⅰ)求橢圓的離心率;
(Ⅱ)設經(jīng)過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與橢圓在
與橢圓在![]() 軸上方的交點為
軸上方的交點為![]() ,圓
,圓![]() 同時與
同時與![]() 軸和直線
軸和直線![]() 相切,圓心
相切,圓心![]() 在直線
在直線![]() 上,且
上,且![]() ,求橢圓的方程.
,求橢圓的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】生活中人們常用“通五經(jīng)貫六藝”形容一個人才識技藝過人,這里的“六藝”其實源于中國周朝的貴族教育體系,具體包括“禮、樂、射、御、書、數(shù)”.為弘揚中國傳統(tǒng)文化,某校在周末學生業(yè)余興趣活動中開展了“六藝”知識講座,每藝安排一節(jié),連排六節(jié),則滿足“數(shù)”必須排在前兩節(jié),“禮”和“樂”必須分開安排的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,正四面體![]() 底面的中心為
底面的中心為![]() ,
,![]() 的重心為
的重心為![]() .
.![]() 是
是![]() 內(nèi)部一動點(包括邊界),滿足
內(nèi)部一動點(包括邊界),滿足![]() ,
,![]() ,
,![]() 不共線且點
不共線且點![]() 到點
到點![]() 的距離與到平面
的距離與到平面![]() 的距離相等.
的距離相等.
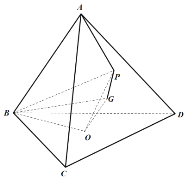
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,求四面體
,求四面體![]() 體積的最大值.
體積的最大值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com