
【題目】如圖,正四面體![]() 底面的中心為
底面的中心為![]() ,
,![]() 的重心為
的重心為![]() .
.![]() 是
是![]() 內部一動點(包括邊界),滿足
內部一動點(包括邊界),滿足![]() ,
,![]() ,
,![]() 不共線且點
不共線且點![]() 到點
到點![]() 的距離與到平面
的距離與到平面![]() 的距離相等.
的距離相等.
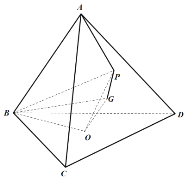
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,求四面體
,求四面體![]() 體積的最大值.
體積的最大值.
【答案】(1)證明見解析;(2)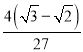 .
.
【解析】
![]() 1
1![]() 延長AG交BC于M,則M為BC的中點,由于O是
延長AG交BC于M,則M為BC的中點,由于O是![]() 的重心,從而
的重心,從而![]() ,由此能證明
,由此能證明![]() 平面OPG.
平面OPG.
![]() 2
2![]() 作
作![]() 于Q點,可證得
于Q點,可證得![]() 平面ABM,則
平面ABM,則![]() ,作P到底面上的投影H,則
,作P到底面上的投影H,則![]() 于
于![]() ,由三垂線定理得
,由三垂線定理得![]() ,從而
,從而![]() ,由橢圓的第二定義得P點的軌跡是以A為右焦點,直線CD為右準線的橢圓,由橢圓的對稱性得當P與
,由橢圓的第二定義得P點的軌跡是以A為右焦點,直線CD為右準線的橢圓,由橢圓的對稱性得當P與![]() 重合時,
重合時,![]() 最大,由此能求出四面體
最大,由此能求出四面體![]() 體積的最大值.
體積的最大值.
(1)證明:如圖,
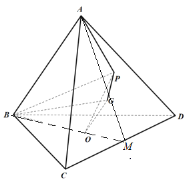
延長AG交BC于M,則M為BC的中點,
由于O是![]() 的重心,則B、O、M共線,
的重心,則B、O、M共線,
且![]() ,
,
![]() ,
,
又A,P,G三點不共線,則P不在平面ABOG內部,
則![]() 平面OPG.
平面OPG.
![]() 2
2![]() 作
作![]() 于Q點,
于Q點,
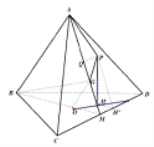
由![]() ,
,![]() ,得
,得![]() 平面ABM,
平面ABM,
又![]() ,則
,則![]() 平面ABM,
平面ABM,
則![]() ,
,
下面求PQ的最大值,
作P到底面上的投影H,
則![]() 于
于![]() ,
,
由三垂線定理得![]() ,
,
則![]() ,
,
由![]() ,得
,得![]() ,
,
接下來,分析在平面ACD中![]() 的最小值,
的最小值,
由于![]() ,
,
由橢圓的第二定義得P點的軌跡是以A為右焦點,直線CD為右準線的橢圓,
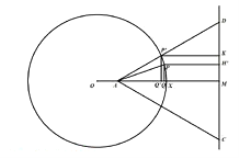
由橢圓的對稱性得當P與![]() 重合時,
重合時,![]() 最大,
最大,
此時,設![]() ,則
,則![]() ,
,
![]() ,
,
則![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() 四面體
四面體![]() 體積
體積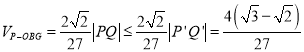 .
.
![]() 四面體
四面體![]() 體積的最大值為
體積的最大值為 .
.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,函數
,函數![]() 在點
在點![]() 處的切線斜率為0.
處的切線斜率為0.
(1)試用含有![]() 的式子表示
的式子表示![]() ,并討論
,并討論![]() 的單調性;
的單調性;
(2)對于函數![]() 圖象上的不同兩點
圖象上的不同兩點![]() ,
,![]() ,如果在函數
,如果在函數![]() 圖象上存在點
圖象上存在點![]() ,使得在點
,使得在點![]() 處的切線
處的切線![]() ,則稱
,則稱![]() 存在“跟隨切線”.特別地,當
存在“跟隨切線”.特別地,當![]() 時,又稱
時,又稱![]() 存在“中值跟隨切線”.試問:函數
存在“中值跟隨切線”.試問:函數![]() 上是否存在兩點
上是否存在兩點![]() 使得它存在“中值跟隨切線”,若存在,求出
使得它存在“中值跟隨切線”,若存在,求出![]() 的坐標,若不存在,說明理由.
的坐標,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學高三數學奧林匹克競賽集訓隊的一次數學測試成績的莖葉圖(圖1)和頻率分布直方圖(圖2)都受到不同程度的破壞,可見部分如圖所示,據此解答如下問題.
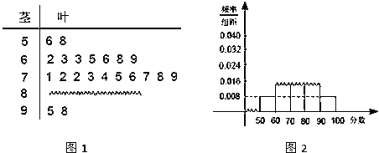
(1)求該集訓隊總人數及分數在[80,90)之間的頻數;
(2)計算頻率分布直方圖中[80,90)的矩形的高;
(3)若要從分數在[80,100]之間的試卷中任取兩份分析學生的答題情況,在抽取的試卷中,求至少有一份分數在[90,100]之間的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】密云某商場舉辦春節優惠酬賓贈券活動,購買百元以上單件商品可以使用優惠劵一張,并且每天購物只能用一張優惠券.一名顧客得到三張優惠券,三張優惠券的具體優惠方式如下:
優惠券1:若標價超過50元,則付款時減免標價的10%;
優惠券2:若標價超過100元,則付款時減免20元;
優惠券3:若標價超過100元,則超過100元的部分減免18%.
如果顧客需要先用掉優惠券1,并且使用優惠券1比使用優惠券2、優惠券3減免的都多,那么你建議他購買的商品的標價可以是__________元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三人獨立地對某一技術難題進行攻關.甲能攻克的概率為![]() ,乙能攻克的概率為
,乙能攻克的概率為![]() ,丙能攻克的概率為
,丙能攻克的概率為![]() .
.
(1)求這一技術難題被攻克的概率;
(2)現假定這一技術難題已被攻克,上級決定獎勵![]() 萬元.獎勵規則如下:若只有一人攻克,則此人獲得全部獎金
萬元.獎勵規則如下:若只有一人攻克,則此人獲得全部獎金![]() 萬元;若只有兩人攻克,則獎金獎給此二人,每人各得
萬元;若只有兩人攻克,則獎金獎給此二人,每人各得![]() 萬元;若三人均攻克,則獎金獎給此三人,每人各得
萬元;若三人均攻克,則獎金獎給此三人,每人各得![]() 萬元.設乙、丙兩人得到的獎金數的和為X,求X的分布列和均值.
萬元.設乙、丙兩人得到的獎金數的和為X,求X的分布列和均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】秉承“綠水青山就是金山銀山”的發展理念,某市環保部門通過制定評分標準,先對本市的企業進行評估,評出四個等級,并根據等級給予相應的獎懲,如下表所示:
評估得分 |
|
|
|
|
評定等級 | 不合格 | 合格 | 良好 | 優秀 |
獎勵(萬元) |
|
|
|
|
環保部門對企業評估完成后,隨機抽取了![]() 家企業的評估得分(
家企業的評估得分(![]() 分)為樣本,得到如下頻率分布表:
分)為樣本,得到如下頻率分布表:
評估得分 |
|
|
|
|
|
|
頻率 |
|
|
|
|
|
|
其中![]() 、
、![]() 表示模糊不清的兩個數字,但知道樣本評估得分的平均數是
表示模糊不清的兩個數字,但知道樣本評估得分的平均數是![]() .
.
(1)現從樣本外的數百個企業評估得分中隨機抽取![]() 個,若以樣本中頻率為概率,求該家企業的獎勵不少于
個,若以樣本中頻率為概率,求該家企業的獎勵不少于![]() 萬元的概率;
萬元的概率;
(2)現從樣本“不合格”、“合格”、“良好”三個等級中,按分層抽樣的方法抽取![]() 家企業,再從這
家企業,再從這![]() 家企業隨機抽取
家企業隨機抽取![]() 家,求這兩家企業所獲獎勵之和不少于
家,求這兩家企業所獲獎勵之和不少于![]() 萬元的概率.
萬元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某建筑工地搭建的腳手架局部類似于一個3×2×3的長方體框架,一個建筑工人欲從A處沿腳手架攀登至B處,則其最近的行走路線中不連續向上攀登的概率為( )
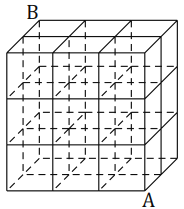
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電視傳媒公司為了解某地區觀眾對某體育節目的收視情況,隨機抽取了100名觀眾進行調查,其中女性有55名,下面是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖:
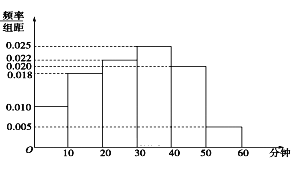
將日均收看該體育節目時間不低于40分鐘的觀眾稱為“體育迷”.
(1)根據已知條件完成下面的22列聯表,并據此資料你是否認為“體育迷”與性別有關?
非體育迷 | 體育迷 | 合計 | |
男 | |||
女 | 10 | 55 | |
合計 |
(2)將上述調查所得到的頻率視為概率.現在從該地區大量電視觀眾中,采用隨機抽樣方法每次抽取1名觀眾,抽取3次,記被抽取的3名觀眾中的“體育迷”人數為X.若每次抽取的結果是相互獨立的,求X的分布列,期望E(X)和方差D(X).
附:![]() .
.
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com