
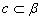
解法一:(反證法)
假設MN與PQ共面于β,則點M、N、P、Q∈β.
又點N、Q∈b![]()
![]()
![]()
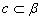 ,同理
,同理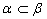 ,∴a、b、C共面,與已知a、b、C不共面矛盾,故MN與PQ為異面直線.
,∴a、b、C共面,與已知a、b、C不共面矛盾,故MN與PQ為異面直線.
解法二:
![]() 點Q
點Q![]() MN.
MN.
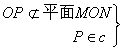
![]() 點P
點P![]() 平面MON.
平面MON.
故平面MON內一點Q與平面外一點P的連線PQ,與平面內不過Q點的直線MN是異面直線.
點評:(1)證明兩條直線異面通常用反證法,反證法是一種間接證法,在立體幾何證題中經常用到,在運用反證法時,一定要嚴格按照步驟分層次進行.
(2)利用反證法證明兩條直線異面,有兩種假設:一是假設兩直線共面;二是假設兩直線平行或相交,必須指出,后一種假設往往不如前一種假設優越.
(3)定理法也是判斷兩直線異面的一種重要方法,運用時,要積極尋找定理的條件.


科目:高中數學 來源: 題型:
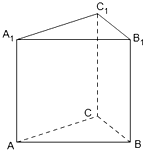 如圖,已知A,B,C為不在同一直線上的三點,且AA1∥BB1∥CC1,AA1=BB1=CC1.
如圖,已知A,B,C為不在同一直線上的三點,且AA1∥BB1∥CC1,AA1=BB1=CC1.查看答案和解析>>
科目:高中數學 來源:2008-2009學年寧夏銀川市六盤山中學高一(下)第二次月考數學試卷(必修2)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com