
【題目】已知函數![]() ,
,![]() ,其中
,其中![]() ,設
,設![]() .
.
(1)判斷![]() 的奇偶性,并說明理由;
的奇偶性,并說明理由;
(2)若![]() ,求使
,求使![]() 成立的x的集合
成立的x的集合
【答案】(1)奇函數;(2){x|0<x<1}
【解析】
(1)依題意得1+x>0,1-x>0,
∴函數h(x)的定義域為(-1,1).
∵對任意的x∈(-1,1),-x∈(-1,1),
h(-x)=f(-x)-g(-x)
=loga(1-x)-loga(1+x)
=g(x)-f(x)=-h(x),
∴h(x)是奇函數.
(2)由f(3)=2,得a=2.
此時h(x)=log2(1+x)-log2(1-x),
由h(x)>0即log2(1+x)-log2(1-x)>0,
∴log2(1+x)>log2(1-x).
由1+x>1-x>0,解得0<x<1.
故使h(x)>0成立的x的集合是{x|0<x<1}.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的長軸長為4,離心率為
的長軸長為4,離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過右焦點![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() 兩點,過點
兩點,過點![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() ,連接
,連接![]() ,當直線
,當直線![]() 的傾斜角發生變化時,直線
的傾斜角發生變化時,直線![]() 與
與![]() 軸是否相交于定點?若是,求出定點坐標,否則,說明理由.
軸是否相交于定點?若是,求出定點坐標,否則,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設m,n是兩條不同直線,![]() ,
,![]() ,
,![]() 是三個不同平面,給出下列四個命題:①若m⊥
是三個不同平面,給出下列四個命題:①若m⊥![]() ,n⊥
,n⊥![]() ,則m//n;②若
,則m//n;②若![]() //
//![]() ,
,![]() //
//![]() ,m⊥
,m⊥![]() ,則m⊥
,則m⊥![]() ;③若m//
;③若m//![]() ,n//
,n//![]() ,則m//n;④
,則m//n;④![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,則
,則![]() //
//![]() .其中正確命題的序號是_______.
.其中正確命題的序號是_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】銷售甲、乙兩種商品所得利潤分別是![]() 萬元,它們與投入資金
萬元,它們與投入資金![]() 萬元的關系分別為
萬元的關系分別為![]() ,
,![]() ,(其中
,(其中![]() 都為常數),函數
都為常數),函數![]() 對應的曲線
對應的曲線![]() 、
、![]() 如圖所示.
如圖所示.

(1)求函數![]() 與
與![]() 的解析式;
的解析式;
(2)若該商場一共投資4萬元經銷甲、乙兩種商品,求該商場所獲利潤的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在底面是邊長為6的正方形的四棱錐P--ABCD中,點P在底面的射影H為正方形ABCD的中心,異面直線PB與AD所成角的正切值為![]() ,則四棱錐P--ABCD的內切球與外接球的半徑之比為( )
,則四棱錐P--ABCD的內切球與外接球的半徑之比為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知小明(如圖中![]() 所示)身高
所示)身高![]() 米,路燈
米,路燈![]() 高
高![]() 米,
米, ![]() ,
, ![]() 均垂直于水平地面,分別與地面交于點
均垂直于水平地面,分別與地面交于點![]() ,
, ![]() .點光源從
.點光源從![]() 發出,小明在地上的影子記作
發出,小明在地上的影子記作![]() .
.
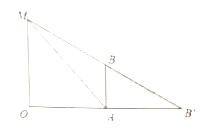
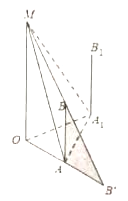
(1)小明沿著圓心為![]() ,半徑為
,半徑為![]() 米的圓周在地面上走一圈,求
米的圓周在地面上走一圈,求![]() 掃過的圖形面積;
掃過的圖形面積;
(2)若![]() 米,小明從
米,小明從![]() 出發,以
出發,以![]() 米/秒的速度沿線段
米/秒的速度沿線段![]() 走到
走到![]() ,
, ![]() ,且
,且![]() 米.
米. ![]() 秒時,小明在地面上的影子長度記為
秒時,小明在地面上的影子長度記為![]() (單位:米),求
(單位:米),求![]() 的表達式與最小值.
的表達式與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在極坐標系中,曲線![]() 的極坐標方程
的極坐標方程![]() .以極點為原點,極軸為
.以極點為原點,極軸為![]() 軸非負半軸建立平面直角坐標系,且在兩坐標系中取相同的長度單位,直線
軸非負半軸建立平面直角坐標系,且在兩坐標系中取相同的長度單位,直線![]() 的參數方程為
的參數方程為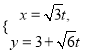 (
(![]() 為參數).
為參數).
(1)寫出曲線![]() 的參數方程和直線
的參數方程和直線![]() 的普通方程;
的普通方程;
(2)過曲線![]() 上任意一點
上任意一點![]() 作與直線
作與直線![]() 相交的直線,該直線與直線
相交的直線,該直線與直線![]() 所成的銳角為
所成的銳角為![]() ,設交點為
,設交點為![]() ,求
,求![]() 的最大值和最小值,并求出取得最大值和最小值時點
的最大值和最小值,并求出取得最大值和最小值時點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com