【題目】已知函數
.
（1）若
，求
的單調區間；
（2）若
是的唯一極值點，求
的取值范圍.
【答案】（1）增區間是
，減區間是
（2）
【解析】
（1）利用導數
，求函數的單調區間；
（2）首先求函數的導數
，令
，轉化為函數
沒有變號零點，求
的取值范圍.
解：（1）由題意可得
當
時，，
因為
，所以
所以
時，
，
時，
.
所以
的增區間是，減區間是.
（2），令
則
，當，
，當，
，
所以在遞減，在遞增，
所以
①當
，即
時，
恒成立，
故時，；時，
故在遞增，在遞減，所以
是的唯一極值點，滿足題意.
②當
.即
時，在遞減，在遞增，
.
故時，
，得；時，，得
故在遞增，在遞減
所以是的唯一極值點，滿足題意.
③當
，
時，
，
，令
，則
，
，
令
，，
令
，，
，故
在
遞增，故
故
在遞增，
，故
所以在存在唯一零點，設為
，
當
時，
，得；當
時，
，得，
所以在
遞減，
遞增，所以
也是的極值點，
所以不符合題意
綜上所述，的取值范圍是
（注：①②可合并）
海淀黃岡名師導航系列答案
普通高中同步練習冊系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，
分別為橢圓
的左，右焦點，直線
過點
與橢圓交于
兩點，當直線的斜率為
時，線段
的長為
.
（1）求橢圓的方程；
（2）過點且與直線垂直的直線
與橢圓交于
兩點，求四邊形
面積的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知一家公司生產某種品牌服裝的年固定成本為
萬元，每生產
千件需另投入
萬元．設該公司一年內共生產該品牌服裝
千件并全部銷售完，每千件的銷售收入為
萬元，且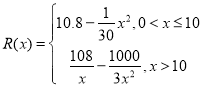
.
（1）寫出年利潤
（萬元）關于年產量（千件）的函數解析式；
（2）年產量為多少千件時，該公司在這一品牌服裝的生產中所獲得利潤最大？（注：年利潤=年銷售收入-年總成本）
查看答案和解析>>
科目：高中數學 來源： 題型：
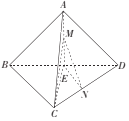
【題目】如圖，在三棱錐A﹣BCD中，點E在BD上，EA＝EB＝EC＝ED，BD
CD，△ACD為正三角形，點M，N分別在AE，CD上運動（不含端點），且AM＝CN，則當四面體C﹣EMN的體積取得最大值
時，三棱錐A﹣BCD的外接球的表面積為_____.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
中，
，前
項和為
，若對任意的
，均有
（
是常數，且
）成立，則稱數列為“
數列”.
（1）若數列為“
數列”，求數列的前項和；
（2）若數列為“
數列”，且
為整數，試問：是否存在數列，使得
對任意
，成立？如果存在，求出這樣數列的的所有可能值，如果不存在，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
