
【題目】已知函數![]() .
.
(1)若![]() ,求函數
,求函數![]() 的單調性;
的單調性;
(2)若![]() 且
且![]() ,求證:
,求證:![]() .
.
【答案】(1)在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;(2)見解析.
上單調遞增;(2)見解析.
【解析】
(1)求導得到導函數后,通過![]() ,確定
,確定![]() 的正負,從而得到函數的單調性;
的正負,從而得到函數的單調性;
(2)將問題轉化為證明:![]() ,設
,設![]() ,只需證
,只需證![]() ;通過求導運算,可知
;通過求導運算,可知![]() ,再通過零點存在定理,不斷確定
,再通過零點存在定理,不斷確定![]() 的最值位置,從而證得
的最值位置,從而證得![]() ,證得結論.
,證得結論.
(1)函數![]() 的定義域為
的定義域為![]() ,
,
![]()
因為![]() ,所以
,所以![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
(2)若![]() 且
且![]() ,
,
欲證![]() ,只需證
,只需證![]() ,
,
即證![]() ,
,
設函數![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,
所以函數![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() ,
,
設函數![]() ,則
,則![]() ,
,
設函數![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,
故![]() ,使得
,使得![]() ,
,
從而函數![]() 在
在![]() 上單調增,在
上單調增,在![]() 上單調減,
上單調減,
所以![]() ,且
,且![]() ,
,
故存在![]() ,使得
,使得![]() ,
,
即當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
從而函數![]() 在
在![]() 上單調增,在
上單調增,在![]() 上單調減,
上單調減,
因為![]() ,故當
,故當![]() 時,
時,![]() ,
,
所以![]() ,
,
即![]() .
.


科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,不與坐標軸垂直的直線
,不與坐標軸垂直的直線![]() 與拋物線交于
與拋物線交于![]() 兩點,當
兩點,當![]() 且
且![]() 時,
時,![]() .
.
(1)求拋物線的標準方程;
(2)若![]() 過定點
過定點![]() ,點
,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,證明:直線
,證明:直線![]() 過定點,并求出定點坐標.
過定點,并求出定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為了改善居民的休閑娛樂活動場所,現有一塊矩形![]() 草坪如下圖所示,已知:
草坪如下圖所示,已知:![]() 米,
米,![]() 米,擬在這塊草坪內鋪設三條小路
米,擬在這塊草坪內鋪設三條小路![]() 、
、![]() 和
和![]() ,要求點
,要求點![]() 是
是![]() 的中點,點
的中點,點![]() 在邊
在邊![]() 上,點
上,點![]() 在邊
在邊![]() 時上,且
時上,且![]() .
.
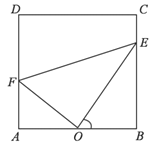
(1)設![]() ,試求
,試求![]() 的周長
的周長![]() 關于
關于![]() 的函數解析式,并求出此函數的定義域;
的函數解析式,并求出此函數的定義域;
(2)經核算,三條路每米鋪設費用均為![]() 元,試問如何設計才能使鋪路的總費用最低?并求出最低總費用.
元,試問如何設計才能使鋪路的總費用最低?并求出最低總費用.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應國家“精準扶貧、精準脫貧”的號召,某貧困縣在精準推進上下功夫,在精準扶貧上見實效.根據當地氣候特點大力發展中醫藥產業,藥用昆蟲的使用相應愈來愈多,每年春暖以后到寒冬前,昆蟲大量活動與繁殖,易于采取各種藥用昆蟲.已知一只藥用昆蟲的產卵數![]() (單位:個)與一定范圍內的溫度
(單位:個)與一定范圍內的溫度![]() (單位:
(單位:![]() )有關,于是科研人員在
)有關,于是科研人員在![]() 月份的
月份的![]() 天中隨機選取了
天中隨機選取了![]() 天進行研究,現收集了該種藥物昆蟲的
天進行研究,現收集了該種藥物昆蟲的![]() 組觀察數據如表:
組觀察數據如表:
日期 |
|
|
|
|
|
溫度 |
|
|
|
|
|
產卵數 |
|
|
|
|
|
(1)從這![]() 天中任選
天中任選![]() 天,記這
天,記這![]() 天藥用昆蟲的產卵數分別為
天藥用昆蟲的產卵數分別為![]() 、
、![]() ,求“事件
,求“事件![]() ,
,![]() 均不小于
均不小于![]() ”的概率?
”的概率?
(2)科研人員確定的研究方案是:先從這![]() 組數據中任選
組數據中任選![]() 組,用剩下的
組,用剩下的![]() 組數據建立線性回歸方程,再對被選取的
組數據建立線性回歸方程,再對被選取的![]() 組數據進行檢驗.
組數據進行檢驗.
①若選取的是![]() 月
月![]() 日與
日與![]() 月
月![]() 日這
日這![]() 組數據,請根據
組數據,請根據![]() 月
月![]() 日、
日、![]() 日和
日和![]() 日這三組數據,求出
日這三組數據,求出![]() 關于
關于![]() 的線性回歸方程?
的線性回歸方程?
②若由線性回歸方程得到的估計數據與所選出的檢驗數據的差的絕對值均不超過![]() 個,則認為得到的線性回歸方程是可靠的,試問①中所得的線性回歸方程是否可靠?
個,則認為得到的線性回歸方程是可靠的,試問①中所得的線性回歸方程是否可靠?
附公式:![]() ,
,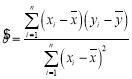 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com