
【題目】如圖,在直角梯形![]() 中,
中,![]() ,平面
,平面![]() 外一點
外一點![]() 在平
在平![]() 內的射影
內的射影![]() 恰在邊
恰在邊![]() 的中點
的中點![]() 上,
上,![]() .
.
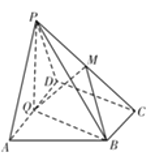
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 在線段
在線段![]() 上,且
上,且![]() 平面
平面![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)推導出PQ⊥平面ABCD,PQ⊥AD,CD∥BQ,從而BQ⊥AD,進而AD⊥平面PBQ,由此能證明平面PQB⊥平面PAD.
(2)連接AC與BQ交于點N,則N為AC中點,則點M到平面PAB的距離是點C到平面PAB的距離的![]() ,求出三棱錐P-ABC的體積V=
,求出三棱錐P-ABC的體積V=![]() ,PAB的面積為
,PAB的面積為![]() ,設點M到平面PAB的距離為d,由VC-PAB=VP-ABC,能求出點M到平面PAB的距離.
,設點M到平面PAB的距離為d,由VC-PAB=VP-ABC,能求出點M到平面PAB的距離.
(1)∵P在平面ABCD內的射影Q恰在邊AD上,
∴PQ⊥平面ABCD,
∵AD平面ABCD,∴PQ⊥AD,
∵Q為線段AD中點,
∴CD∥BQ,∴BQ⊥AD,∴AD⊥平面PBQ,AD平面PAD,
∴平面PQB⊥平面PAD.
(2)連接AC與BQ交于點N,則N為AC中點,

∴點M到平面PAB的距離是點C到平面PAB的距離的![]() ,
,
在三棱錐P-ABC中,高PQ=![]() ,底面積為
,底面積為![]() ,
,
∴三棱錐P-ABC的體積V=![]() =
=![]() ,
,
又△PAB中,PA=AB=2,PB=![]() ,
,
∴△PAB的面積為![]() ,
,
設點M到平面PAB的距離為d,
由VC-PAB=VP-ABC,得![]() =
=![]() ,
,
解得d=![]() ,
,
∴點M到平面PAB的距離為![]() .
.


 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的長軸長是短軸長的2倍,且過點
的長軸長是短軸長的2倍,且過點![]() .
.
⑴求橢圓![]() 的方程;
的方程;
⑵若在橢圓上有相異的兩點![]() (
(![]() 三點不共線),
三點不共線),![]() 為坐標原點,且直線
為坐標原點,且直線![]() ,直線
,直線![]() ,直線
,直線![]() 的斜率滿足
的斜率滿足![]() .
.
(ⅰ)求證: ![]() 是定值;
是定值;
(ⅱ)設![]() 的面積為
的面積為![]() ,當
,當![]() 取得最大值時,求直線
取得最大值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,已知曲線 (
(![]() 為參數),
為參數),![]() .以原點
.以原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(I)寫出曲線![]() 與圓
與圓![]() 的極坐標方程;
的極坐標方程;
(II)在極坐標系中,已知射線![]() 分別與曲線
分別與曲線![]() 及圓
及圓![]() 相交于
相交于![]() ,當
,當![]() 時,求
時,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]()
![]() 的焦點為
的焦點為![]() ,直線
,直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,與拋物線
,與拋物線![]() 的交點為
的交點為![]() ,且
,且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)過拋物線![]() 上一點
上一點![]() 作兩條互相垂直的弦
作兩條互相垂直的弦![]() 和
和![]() ,試問直線
,試問直線![]() 是否過定點,若是,求出該定點;若不是,請說明理由.
是否過定點,若是,求出該定點;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,圓錐的頂點為A,底面的圓心為O,BC是底面圓的一條直徑,點D,E在底面圓上,已知![]() ,
,![]() .
.
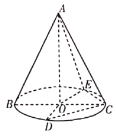
(1)證明:![]() ;
;
(2)若二面角![]() 的大小為
的大小為![]() ,求直線OC與平面ACE所成角的正弦值.
,求直線OC與平面ACE所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為自然對數的底數).
為自然對數的底數).
(1)若曲線![]() 在點
在點![]() (處的切線與曲線
(處的切線與曲線![]() 在點
在點![]() 處的切線互相垂直,求函數
處的切線互相垂直,求函數![]() 在區間
在區間![]() 上的最大值;
上的最大值;
(2)設函數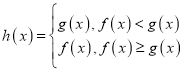 ,試討論函數
,試討論函數![]() 零點的個數.
零點的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市為了解顧客的購物量及結算時間等信息,安排一名員工隨機收集了在該超市購物的100位顧客的相關數據,統計結果如下表所示,已知這100位顧客中一次購物量超過7件的顧客占![]() .
.
一次購物量 | 1至3件 | 4至7件 | 8至11件 | 12至15件 | 16件及以上 |
顧客數(人) |
| 27 | 20 |
| 10 |
結算時間( | 0.5 | 1 | 1.5 | 2 | 2.5 |
(1)確定![]() ,
,![]() 的值,并求顧客一次購物的結算時間的平均值;
的值,并求顧客一次購物的結算時間的平均值;
(2)從收集的結算時間不超過![]() 的顧客中,按分層抽樣的方法抽取5人,再從這5人中隨機抽取2人,求至少有1人的結算時間為
的顧客中,按分層抽樣的方法抽取5人,再從這5人中隨機抽取2人,求至少有1人的結算時間為![]() 的概率.(注:將頻率視為概率)
的概率.(注:將頻率視為概率)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程:在直角坐標系![]() 中,曲線
中,曲線![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)已知點![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() ,它與曲線
,它與曲線![]() 的交點為
的交點為![]() ,
,![]() ,與曲線
,與曲線![]() 的交點為
的交點為![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com