
【題目】已知拋物線![]() :
:![]()
![]() 的焦點為
的焦點為![]() ,直線
,直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,與拋物線
,與拋物線![]() 的交點為
的交點為![]() ,且
,且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)過拋物線![]() 上一點
上一點![]() 作兩條互相垂直的弦
作兩條互相垂直的弦![]() 和
和![]() ,試問直線
,試問直線![]() 是否過定點,若是,求出該定點;若不是,請說明理由.
是否過定點,若是,求出該定點;若不是,請說明理由.
【答案】(1)![]() (2)直線
(2)直線![]() 恒過定點
恒過定點![]()
【解析】
(1)設(shè)![]() ,代入拋物線方程,結(jié)合拋物線的定義,可得
,代入拋物線方程,結(jié)合拋物線的定義,可得![]() ,進(jìn)而得到拋物線方程;
,進(jìn)而得到拋物線方程;
(2)由題可得![]() ,直線
,直線![]() 的斜率不為
的斜率不為![]() ,設(shè)直線
,設(shè)直線![]() :
:![]() ,
,![]() ,
,![]() ,聯(lián)立直線與曲線方程,由
,聯(lián)立直線與曲線方程,由![]() ,則
,則![]() ,即可得到
,即可得到![]() ,
,![]() 的關(guān)系式,再求出直線過定點;
的關(guān)系式,再求出直線過定點;
解:(1)設(shè)![]() ,代入
,代入![]() 得:
得:![]() ,即
,即![]()
由![]() 得:
得:![]() ,解得:
,解得:![]() 或
或![]() (舍去)
(舍去)
故拋物線C的方程為:![]() .
.
(2)由題可得![]() ,直線
,直線![]() 的斜率不為
的斜率不為![]()
設(shè)直線![]() :
:![]() ,
,![]() ,
,![]()
聯(lián)立![]() ,得:
,得:![]() ,
,
![]() ,
,![]() ,
,![]()
由![]() ,則
,則![]() ,即
,即![]() .
.
于是![]()
![]()
![]() ,所以
,所以![]()
![]() 或
或![]()
當(dāng)![]() 時,
時,![]()
直線![]() :
:![]() ,恒過定點
,恒過定點![]() ,不合題意,舍去.
,不合題意,舍去.
當(dāng)![]() ,
,![]() ,直線
,直線![]() :
:![]() ,恒過定點
,恒過定點![]()
綜上可知,直線![]() 恒過定點
恒過定點![]()


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,點
,點![]() 也為拋物線
也為拋物線![]() 的焦點.(1)若
的焦點.(1)若![]() 為橢圓
為橢圓![]() 上兩點,且線段
上兩點,且線段![]() 的中點為
的中點為![]() ,求直線
,求直線![]() 的斜率;
的斜率;
(2)若過橢圓![]() 的右焦點
的右焦點![]() 作兩條互相垂直的直線分別交橢圓于
作兩條互相垂直的直線分別交橢圓于![]() 和
和![]() ,設(shè)線段
,設(shè)線段![]() 的長分別為
的長分別為![]() ,證明
,證明![]() 是定值.
是定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過年時小明的舅舅在家庭微信群里發(fā)了一個10元的紅包,紅包被隨機(jī)分配為2.51元,3.32元,1.24元,0.26元,2.67元,共五份.現(xiàn)已知小明與爸爸都各自搶到了一個紅包,則兩人搶到紅包的金額總和不小于4元的概率為__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“割圓術(shù)”是劉徽最突出的數(shù)學(xué)成就之一,他在《九章算術(shù)注》中提出割圓術(shù),并作為計算圓的周長,面積已經(jīng)圓周率的基礎(chǔ),劉徽把圓內(nèi)接正多邊形的面積一直算到了正3072邊形,并由此而求得了圓周率為3.1415和3.1416這兩個近似數(shù)值,這個結(jié)果是當(dāng)時世界上圓周率計算的最精確數(shù)據(jù).如圖,當(dāng)分割到圓內(nèi)接正六邊形時,某同學(xué)利用計算機(jī)隨機(jī)模擬法向圓內(nèi)隨機(jī)投擲點,計算得出該點落在正六邊形內(nèi)的頻率為0.8269,那么通過該實驗計算出來的圓周率近似值為(參考數(shù)據(jù):![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求函數(shù)![]() 的解析式,并證明:
的解析式,并證明:![]() .
.
(2)已知![]() ,且函數(shù)
,且函數(shù)![]() 與函數(shù)
與函數(shù)![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點,且線段
兩點,且線段![]() 的中點為
的中點為![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的圖象過點
的圖象過點![]() ,且在點
,且在點![]() 處的切線與直線
處的切線與直線![]() 平行.
平行.
(1)求實數(shù)![]() ,
,![]() 的值;
的值;
(2)若對任意的![]() ,函數(shù)
,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上總不是單調(diào)函數(shù),求實數(shù)
上總不是單調(diào)函數(shù),求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直角梯形![]() 中,
中,![]() ,平面
,平面![]() 外一點
外一點![]() 在平
在平![]() 內(nèi)的射影
內(nèi)的射影![]() 恰在邊
恰在邊![]() 的中點
的中點![]() 上,
上,![]() .
.
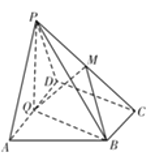
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 在線段
在線段![]() 上,且
上,且![]() 平面
平面![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過點P(3,﹣4)作圓(x﹣1)2+y2=2的切線,切點分別為A,B,則直線AB的方程為( )
A.x+2y﹣2=0B.x﹣2y﹣1=0C.x﹣2y﹣2=0D.x+2y+2=0
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在數(shù)列![]() 中,
中,![]() ,且對任意
,且對任意![]() ,都有
,都有![]() .
.
(1)計算![]() ,
,![]() ,
,![]() ,由此推測
,由此推測![]() 的通項公式,并用數(shù)學(xué)歸納法證明;
的通項公式,并用數(shù)學(xué)歸納法證明;
(2)若![]() (
(![]() ),求無窮數(shù)列
),求無窮數(shù)列![]() 的前
的前![]() 項之和
項之和![]() 與
與![]() 的最大項.
的最大項.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com