【題目】如圖，從參加環(huán)保知識競賽的學生中抽出
名，將其成績（均為整數(shù)）整理后畫出的頻率分布直方圖如下，觀察圖形，回答下列問題：
（1）
這一組的頻數(shù)、頻率分別是多少？
（2）估計這次環(huán)保知識競賽的及格率（分及以上為及格）和平均數(shù)?
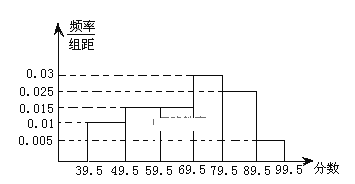
【答案】(1)見解析;(2)0.75;70.5.
【解析】
分析：⑴利用頻率分布直方圖中，縱坐標與組距的乘積是相應的頻率，而頻數(shù)=頻率
組距，可得結論
⑵縱坐標與組距的乘積是相應的頻率，再求和，即可得到結論
詳解：（1）利用頻率分布直方圖中，縱坐標與組距的乘積是相應的頻率，而頻數(shù)=頻率組距，可得結論，頻率為：0.02510=0.25，頻數(shù)為：0.2560=15.
(2)縱坐標與組距的乘積是相應的頻率，再求和，即可得到結論，
1）及格率為：0.01510+0.0310+0.02510+0.00510=0.15+0.3+0.25+0.05=0.75
2）平均數(shù)為：44.50.0110+54.50.01510+64.50.01510+74.50.0310+84.50.02510+94.50.00510=4.45+8.175+9.675+22.35+21.125+4.75=70.5
科目：高中數(shù)學 來源： 題型：
【題目】已知直線
，
（1）系數(shù)為什么值時，方程表示通過原點的直線；
（2）系數(shù)滿足什么關系時與坐標軸都相交；
（3）系數(shù)滿足什么條件時只與x軸相交；
（4）系數(shù)滿足什么條件時是x軸；
（5）設
為直線上一點，證明：這條直線的方程可以寫成
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）=sin2x+sinx+cosx，以下說法中不正確的是（ ）
A.f（x）周期為2π
B.f（x）最小值為﹣ 
C.f（x）在區(qū)間[0， 
]單調(diào)遞增
D.f（x）關于點x= 
對稱
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知直線
： 
， 
： 
，和兩點
（0,1），
（-1,0），給出如下結論：
①不論
為何值時， 
與
都互相垂直；
②當
變化時， 
與
分別經(jīng)過定點A（0,1）和B（-1,0）；
③不論
為何值時， 
與
都關于直線
對稱；
④如果
與
交于點
，則
的最大值是1；
其中，所有正確的結論的個數(shù)是（ ）
A. 1 B. 2 C. 3 D. 4.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
定義在
上且滿足下列兩個條件:
①對任意
都有
;
②當
時,有
，
（1）求
，并證明函數(shù)在上是奇函數(shù)；
（2）驗證函數(shù)
是否滿足這些條件；
（3）若
，試求函數(shù)
的零點.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在數(shù)列{an}中，前n項和為Sn ， 且Sn= 
，數(shù)列{bn}的前n項和為Tn ， 且bn= 
（1）求數(shù)列{an}的通項公式；
（2）是否存在m，n∈N* ， 使得Tn=am ， 若存在，求出所有滿足題意的m，n，若不存在，請說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
．
（1）設
．
①若
，求函數(shù)
的零點；
②若函數(shù)存在零點，求
的取值范圍．
（2）設
，若對任意
恒成立，試求的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知拋物線C1：y2=8ax（a＞0），直線l傾斜角是45°且過拋物線C1的焦點，直線l被拋物線C1截得的線段長是16，雙曲線C2： 
﹣ 
=1的一個焦點在拋物線C1的準線上，則直線l與y軸的交點P到雙曲線C2的一條漸近線的距離是（ ）
A.2
B.
C.
D.1
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
