Question

13．點P是△ABC內一點，且$\overrightarrow{PA}+2\overrightarrow{PB}+3\overrightarrow{PC}=\overrightarrow 0$，則△ABP與△ABC的面積之比是（　　）

• A． 1：5
• B． 1：2
• C． 2：5
• D． 1：3

Answer 1

分析 可延長PB到B′，延長PC到C′，并分別使PB′=2PB，PC′=3PC，從而根據條件便得到$\overrightarrow{PA}+\overrightarrow{PB′}+\overrightarrow{PC′}$=$\overrightarrow{0}$，這便說明P為△AB′C′的重心．這便得到三角形PAB′，三角形PB′C′，及三角形PC′A的面積都相等，設為S，從而會得到S_△ABC=S，這樣便可求出△ABP與△ABC的面積之比．

解答 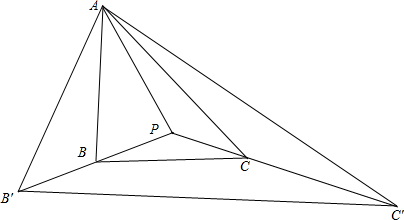解：如圖，延長PB至PB'，使PB'=2PB，延長PC至PC'，使PC'=3PC，并連接AB′，B′C′，C′A，則：$\overrightarrow{PA}+\overrightarrow{PB′}+\overrightarrow{PC′}$=$\overrightarrow{0}$
∴P是△AB′C′的重心；
∴△PAB′，△PB′C′，△PC′A三個三角形的面積相等，記為S；
∴S_△APB=$\frac{S}{2}$，S_△APC=$\frac{S}{3}$，S_△BPC=$\frac{S}{6}$，
∴S_△ABC=S，
∴S_△ABP：S_△ABC=1：2．
故選B．

點評 考查向量數乘的幾何意義，三角形重心和三頂點構成向量的和為零向量，以及三角形的面積公式．