
���}Ŀ����D���������F![]() ��ƽ����߅�Σ�
��ƽ����߅�Σ�![]()
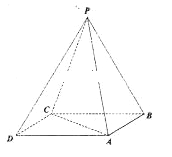
��1���C����ƽ��![]() ƽ��PCD��
ƽ��PCD��
��2����ֱ��PA�cƽ��PCB���ɽǵ�����ֵ��
���𰸡���1��ԔҊ(ji��n)������2��![]()
��������
��1���C��AC![]() ƽ��PCD���Y(ji��)��ƽ���cƽ�洹ֱ�ж������ɡ���2���������gֱ������(bi��o)ϵ���քe�ó�O,P,A,B,C����(bi��o)��Ӌ(j��)��ƽ��PCB�ķ�������Ӌ(j��)������
ƽ��PCD���Y(ji��)��ƽ���cƽ�洹ֱ�ж������ɡ���2���������gֱ������(bi��o)ϵ���քe�ó�O,P,A,B,C����(bi��o)��Ӌ(j��)��ƽ��PCB�ķ�������Ӌ(j��)������![]() ����(bi��o)���Y(ji��)�Ͽ��g������(sh��)���e��Ӌ(j��)�������ɡ�
����(bi��o)���Y(ji��)�Ͽ��g������(sh��)���e��Ӌ(j��)�������ɡ�
�⣨1���C������?y��n)?/span>![]()
����![]()
����![]()
����![]()
��?y��n)?/span>![]() ��
��
����![]()
��?y��n)?/span>![]() ����
����![]()
��2���ɣ�1��֪ ![]()
����![]() ������CD���^(gu��)P��ƽ��PCD��(n��i)��CD�Ĵ����������O��
������CD���^(gu��)P��ƽ��PCD��(n��i)��CD�Ĵ����������O��
ȡBC���c(di��n)��M���BPM,AM��
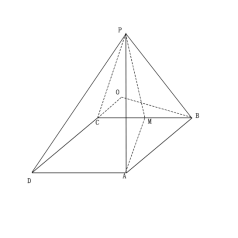
��?y��n)?/span>![]() ,
,![]() ,
,
����![]() ,��
,��![]() ƽ��PAM
ƽ��PAM
����![]() ,
,
��?y��n)?/span> ![]() ,����
,����![]() ,��?y��n)�ֱ��AP
,��?y��n)�ֱ��AP![]() ƽ��PAM,
ƽ��PAM,
����ֱ��![]() ֱ��AP,
ֱ��AP,
��![]() ,����
,����![]() .
.
��![]() �У������Ҷ�����
�У������Ҷ�����![]() ,
,
��![]()
����![]() ,
,
�ɴˣ�![]() ��������߅��ABOC��ƽ����߅�Σ�����
��������߅��ABOC��ƽ����߅�Σ�����![]() ������
������![]()
��ֱ��OP��z�S��ֱ��OD��x�S��ֱ��OB��y�S�������gֱ������(bi��o)ϵ.

����![]()
�O(sh��)![]() ��ƽ��PBC��һ��(g��)����������?y��n)?/span>
��ƽ��PBC��һ��(g��)����������?y��n)?/span>![]()
����![]() ��ȡ
��ȡ![]() ����
����![]() ,
,
����![]() ��
��![]() ,
,
����ֱ��PA�cƽ��PCB���ɽǵ�����ֵ![]() .
.


 ȫ�ܜy(c��)����ĩС��Ԫϵ�д�
ȫ�ܜy(c��)����ĩС��Ԫϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������f(shu��)�����_����( )
A.�ڽy(t��ng)Ӌ(j��)�W(xu��)�У���(d��)���ԙz�(y��n)�Ǚz�(y��n)�ɂ�(g��)���׃���Ƿ����P(gu��n)ϵ��һ�N�y(t��ng)Ӌ(j��)����
B.�ښ���D�У�����ֲ��Ď���^(q��)��Č���Խ�Mխ����ģ�M��Ч��Խ��
C.���Իؚw���̌�(du��)��(y��ng)��ֱ��![]() ���ٽ�(j��ng)�^(gu��)��ӱ���(sh��)��(j��)�c(di��n)�е�һ��(g��)�c(di��n)
���ٽ�(j��ng)�^(gu��)��ӱ���(sh��)��(j��)�c(di��n)�е�һ��(g��)�c(di��n)
D.�ڻؚw�����У����P(gu��n)ָ��(sh��)![]() Խ��ģ�M��Ч��Խ��
Խ��ģ�M��Ч��Խ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�P(gu��n)��x�ĺ���(sh��)![]() ���䌧(d��o)����(sh��)
���䌧(d��o)����(sh��)![]() .
.
��1���������(sh��)![]() ��
��![]() ̎�ИOֵ
̎�ИOֵ![]() ����(sh��)
����(sh��)![]() �ı��_(d��)ʽ��
�ı��_(d��)ʽ��
��2����(d��ng)![]() �r(sh��)������(sh��)
�r(sh��)������(sh��)![]() �ĈD������һ�c(di��n)P̎���о�б�ʞ�k����
�ĈD������һ�c(di��n)P̎���о�б�ʞ�k����![]() ����(sh��)��(sh��)b��ȡֵ����.
����(sh��)��(sh��)b��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() �����ֵ��
�����ֵ��![]() �����ڞ�
�����ڞ�![]() ��������(sh��)
��������(sh��)![]() �ĈD������ƽ��
�ĈD������ƽ��![]() ��(g��)��λ�L(zh��ng)�ȵõ�
��(g��)��λ�L(zh��ng)�ȵõ�![]() �ĈD����
�ĈD����![]() ��ż����(sh��)���t
��ż����(sh��)���t![]() �Ľ���ʽ�飨 ��
�Ľ���ʽ�飨 ��
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ��
��![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() ��
��![]() �ǙE�A
�ǙE�A![]() �ϵ��c(di��n)����
�ϵ��c(di��n)����![]() ����e��
����e��![]() ��
��
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2����б�ʞ�![]() ����
����![]() �S�ϵĽؾ���
�S�ϵĽؾ���![]() ��ֱ��
��ֱ��![]() �c�E�A
�c�E�A![]() �ཻ�ڃ��c(di��n)
�ཻ�ڃ��c(di��n)![]() �����E�A
�����E�A![]() �ϴ����c(di��n)
�ϴ����c(di��n)![]() ���M��
���M��![]() ������
������![]() ������(bi��o)ԭ�c(di��n)����
������(bi��o)ԭ�c(di��n)����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��![]() �����(xi��ng)���f���ȱȔ�(sh��)�У�
�����(xi��ng)���f���ȱȔ�(sh��)�У�![]() ��ӛ��(sh��)��
��ӛ��(sh��)��![]() ��ǰn�(xi��ng)�͞�
��ǰn�(xi��ng)�͞�![]() ���tʹ����ʽ2018
���tʹ����ʽ2018![]() ���������������(sh��)n��ֵ�飨 ��
���������������(sh��)n��ֵ�飨 ��
A. 5 B. 6 C. 7 D. 8
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() .
.
��1����(d��ng)�r(sh��)![]() �����P(gu��n)��
�����P(gu��n)��![]() �IJ���ʽ
�IJ���ʽ![]() ���������
���������![]() ��ȡֵ������
��ȡֵ������
��2����(d��ng)![]() �r(sh��)���C����
�r(sh��)���C����![]()
![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��ʾ���������F![]() �У�����
�У�����![]() �����Σ�
������![]() ����
����![]() ���c(di��n)
���c(di��n)![]() ��
��![]() �ϵ�һ��(g��)��(d��ng)�c(di��n)��
�ϵ�һ��(g��)��(d��ng)�c(di��n)��![]() ��
��![]() .
.

��1����(d��ng)![]() �r(sh��)�����C��
�r(sh��)�����C��![]() ��
��
��2����(d��ng)![]() ƽ��
ƽ��![]() �r(sh��)��������
�r(sh��)��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D,����![]() ��߅�L(zh��ng)��6,
��߅�L(zh��ng)��6, ![]() ,
,![]() .������
.������![]() �،�(du��)�Ǿ�
�،�(du��)�Ǿ�![]() ����,�õ������F
����,�õ������F![]() ,�c(di��n)
,�c(di��n)![]() ����
����![]() �����c(di��n),
�����c(di��n), ![]() .
.

�������C��![]() ��ƽ��
��ƽ��![]() ;
;
�����������F![]() ���w�e.
���w�e.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com