
【題目】已知![]() ,點
,點![]() 在第一象限,以
在第一象限,以![]() 為直徑的圓與
為直徑的圓與![]() 軸相切,動點
軸相切,動點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若曲線![]() 在點
在點![]() 處的切線的斜率為
處的切線的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,求滿足
,求滿足![]() 的點
的點![]() 的個數.
的個數.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知直線x=﹣2上有一動點Q,過點Q作直線l,垂直于y軸,動點P在l1上,且滿足![]() (O為坐標原點),記點P的軌跡為C.
(O為坐標原點),記點P的軌跡為C.
(1)求曲線C的方程;
(2)已知定點M(![]() ,0),N(
,0),N(![]() ,0),點A為曲線C上一點,直線AM交曲線C于另一點B,且點A在線段MB上,直線AN交曲線C于另一點D,求△MBD的內切圓半徑r的取值范圍.
,0),點A為曲線C上一點,直線AM交曲線C于另一點B,且點A在線段MB上,直線AN交曲線C于另一點D,求△MBD的內切圓半徑r的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小明下班回家途經3個有紅綠燈的路口,交通法規定:若在路口遇到紅燈,需停車等待;若在路口沒遇到紅燈,則直接通過.經長期觀察發現:他在第一個路口遇到紅燈的概率為![]() ,在第二、第三個道口遇到紅燈的概率依次減小,在三個道口都沒遇到紅燈的概率為
,在第二、第三個道口遇到紅燈的概率依次減小,在三個道口都沒遇到紅燈的概率為![]() ,在三個道口都遇到紅燈的概率為
,在三個道口都遇到紅燈的概率為![]() ,且他在各路口是否遇到紅燈相互獨立.
,且他在各路口是否遇到紅燈相互獨立.
(1)求小明下班回家途中至少有一個道口遇到紅燈的概率;
(2)求小明下班回家途中在第三個道口首次遇到紅燈的概率;
(3)記![]() 為小明下班回家途中遇到紅燈的路口個數,求數學期望
為小明下班回家途中遇到紅燈的路口個數,求數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某投資公司在![]() 年年初準備將
年年初準備將![]() 萬元投資到“低碳”項目上,現有兩個項目供選擇:
萬元投資到“低碳”項目上,現有兩個項目供選擇:
項目一:新能源汽車.據市場調研,投資到該項目上,到年底可能獲利![]() ,也可能虧損
,也可能虧損![]() ,且這兩種情況發生的概率分別為
,且這兩種情況發生的概率分別為![]() 和
和![]() ;
;
項目二:通信設備.據市場調研,投資到該項目上,到年底可能獲利![]() ,可能損失
,可能損失![]() ,也可能不賠不賺,且這三種情況發生的概率分別為
,也可能不賠不賺,且這三種情況發生的概率分別為![]() 、
、![]() 和
和![]() .
.
針對以上兩個投資項目,請你為投資公司選擇一個合理的項目,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中有如下問題:今有蒲生一日,長三尺,莞生一日,長1尺.蒲生日自半,莞生日自倍.問幾何日而長等?意思是:今有蒲第一天長高3尺,莞第一天長高1尺,以后蒲每天長高前一天的一半,莞每天長高前一天的2倍.若蒲、莞長度相等,則所需時間為()
(結果精確到0.1.參考數據:lg2=0.3010,lg3=0.4771.)
A.2.6天B.2.2天C.2.4天D.2.8天
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]()
![]() 中,對任何正整數n都有:
中,對任何正整數n都有: ![]()
(1)若數列![]() 是首項和公差都是1的等差數列,求證:數列
是首項和公差都是1的等差數列,求證:數列![]() 是等比數列;
是等比數列;
(2)若數列![]() 是首項為1的等比數列,數列
是首項為1的等比數列,數列![]() 是否是等差數列?若是請求出通項公式.
是否是等差數列?若是請求出通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的焦距是
的焦距是![]() ,長軸長是短軸長3倍,任作斜率為
,長軸長是短軸長3倍,任作斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(如圖所示),且點
兩點(如圖所示),且點![]() 在直線
在直線![]() 的左上方.
的左上方.

(1)求橢圓![]() 的方程;
的方程;
(2)若![]() ,求
,求![]() 的面積;
的面積;
(3)證明:![]() 的內切圓的圓心在一條定直線上。
的內切圓的圓心在一條定直線上。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了使房價回歸到收入可支撐的水平,讓全體人民住有所居,近年來全國各一、二線城市打擊投機購房,陸續出臺了住房限購令.某市一小區為了進一步了解已購房民眾對市政府岀臺樓市限購令的認同情況,隨機抽取了本小區50戶住戶進行調查,各戶人平均月收入(單位:千元)的戶數頻率分布直方圖如圖,其中贊成限購的戶數如下表:
人平均月收入 |
|
|
|
|
|
|
贊成戶數 | 4 | 9 | 12 | 6 | 3 | 1 |
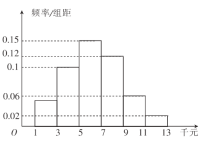
(1)若從人平均月收入在![]() 的住戶中再隨機抽取兩戶,求所抽取的兩戶至少有一戶贊成樓市限購令的概率;
的住戶中再隨機抽取兩戶,求所抽取的兩戶至少有一戶贊成樓市限購令的概率;
(2)若將小區人平均月收入不低于7千元的住戶稱為“高收入戶”,人平均月收入低于7千元的住戶稱為“非高收入戶”根據已知條件完成如圖所給的![]() 列聯表,并說明能否有
列聯表,并說明能否有![]() 的把握認為“收入的高低”與“贊成樓市限購令”有關.
的把握認為“收入的高低”與“贊成樓市限購令”有關.
非高收入戶 | 高收入戶 | ||
贊成 | |||
不贊成 | |||
總計 |
附:臨界值表
| 0.1 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.63.5 | 10.828 |
參考公式: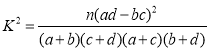 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com