
已知過拋物線y2 =2px(p>0)的焦點F的直線x-my+m=0與拋物線交于A,B兩點,且△OAB(O為坐標原點)的面積為2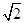 ,則m6+ m4的值為( )
,則m6+ m4的值為( )
A.1 B. 2 C.3 D.4
B
【解析】
試題分析:由題意,可知該拋物線的焦點為 ,它過直線,代入直線方程,可知:
,它過直線,代入直線方程,可知:
 求得
求得
∴直線方程變為:
A,B兩點是直線與拋物線的交點,
∴它們的坐標都滿足這兩個方程.
∴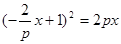
∴
∴方程的解 ,
,
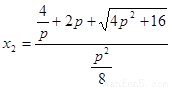 ;
;
代入直線方程,可知: ,
,
 ,
,
△OAB的面積可分為△OAP與△OBP的面積之和,
而△OAP與△OBP若以OP為公共底,
則其高即為A,B兩點的y軸坐標的絕對值,
∴△OAP與△OBP的面積之和為:
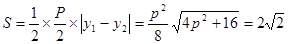
求得p=2,
∵ ,所以
,所以 ,∴
,∴ .
.
故答案為:B
考點:橢圓的簡單性質
點評:本題主要考查了橢圓的簡單性質,直線,拋物線與橢圓的關系.考查了學生綜合分析問題和基本的運算能力.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
| p |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com