若等比數列an滿足anan+1=16n,則公比為( )
A.2
B.4
C.8
D.16
【答案】
分析:令n=1,得到第1項與第2項的積為16,記作①,令n=2,得到第2項與第3項的積為256,記作②,然后利用②÷①,利用等比數列的通項公式得到關于q的方程,求出方程的解即可得到q的值,然后把q的值代入經過檢驗得到滿足題意的q的值即可.
解答:解:當n=1時,a
1a
2=16①;當n=2時,a
2a
3=256②,
②÷①得:
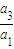
=16,即q
2=16,解得q=4或q=-4,
當q=-4時,由①得:a
12×(-4)=16,即a
12=-4,無解,所以q=-4舍去,
則公比q=4.
故選B
點評:此題考查學生掌握等比數列的性質,靈活運用等比數列的通項公式化簡求值,是一道基礎題.學生在求出q的值后,要經過判斷得到滿足題意的q的值,即把q=-4舍去.

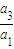 =16,即q2=16,解得q=4或q=-4,
=16,即q2=16,解得q=4或q=-4,
