
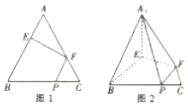
 在邊長為3的正三角形ABC中,E,F,P分別是AB,AC,BC邊上的點,滿足$\frac{AE}{EB}$=$\frac{CF}{FA}$=$\frac{CP}{PB}$=$\frac{1}{2}$,將△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,連結A1B,A1P(如圖),則以下結論錯誤的是( )
在邊長為3的正三角形ABC中,E,F,P分別是AB,AC,BC邊上的點,滿足$\frac{AE}{EB}$=$\frac{CF}{FA}$=$\frac{CP}{PB}$=$\frac{1}{2}$,將△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,連結A1B,A1P(如圖),則以下結論錯誤的是( )| A. | CF∥平面A1EP | |
| B. | A1E⊥平面BEP | |
| C. | 點B到面A1PF的距離為$\sqrt{3}$ | |
| D. | 異面直線BP與A1F所成角的余弦值為$\frac{3}{4}$ |
分析 A,由$\frac{AE}{EB}$=$\frac{CF}{FA}$=$\frac{CP}{PB}$=$\frac{1}{2}$,⇒CF∥EP,⇒CF∥平面A1EP
B,利用面面垂直的性質定理判斷;
C,點B到面A1PF的距離進行轉化,B到面面A1PF的距離即為E到面面A1PF的距離,E到面A1PF的距離即為△A1EF中E到A1F的距離;
D,DF∥BP∴∠DFA1即為所求角
解答 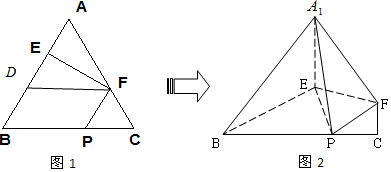 解:對于A,由$\frac{AE}{EB}$=$\frac{CF}{FA}$=$\frac{CP}{PB}$=$\frac{1}{2}$,⇒CF∥EP,⇒CF∥平面A1EP,故正確;
解:對于A,由$\frac{AE}{EB}$=$\frac{CF}{FA}$=$\frac{CP}{PB}$=$\frac{1}{2}$,⇒CF∥EP,⇒CF∥平面A1EP,故正確;
對于B,在圖1中,取BE的中點D,連DF,滿足$\frac{AE}{EB}$=$\frac{CF}{FA}$=$\frac{CP}{PB}$=$\frac{1}{2}$,∵AF=AD=2,又∠A=60°∴△ADF為正三角形
又∵AE=ED=1∴EF⊥AD∴在圖2中有A1E⊥EF,BE=EF
∴∠A1EB為二面角A1-EF-B的平面角∵二面角A1-EF-B為直二面角∴A1E⊥BE
又∵BE∩EF=E,∴A1E⊥面BEF,即A1E⊥面BEP,故正確;
對于C.∵BE∥PF∴BE∥面A1PF,∵B到面面A1PF的距離即為E到面面A1PF的距離,
∵BE⊥面A1EF,又BE∥PF,∴PF⊥面A1EF
∴面A1EF⊥面A1PF∵E到面A1PF的距離即為△A1EF中E到A1F的距離
d=A1E×sin60°=$\frac{\sqrt{3}}{2}$,故錯;
對于D,∵DF∥BP∴∠DFA1即為所求角
△A1DF中A1D=,DF=2,A1F=2,由余弦定理得cos∠DFA1=$\frac{3}{4}$,故正確;
故選:C.
點評 本題考查直線與平面平行、垂直的證明,考查點面距,考查異面直線所成角的余弦值的求法,解題時要認真審題,注意問題的轉化.


科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 60° | B. | 120° | C. | 135° | D. | 150° |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{x^2}{20}-\frac{y^2}{5}=1$ | B. | $\frac{x^2}{20}-\frac{y^2}{100}=1$ | C. | $\frac{x^2}{5}-\frac{y^2}{20}=1$ | D. | $\frac{x^2}{25}-\frac{y^2}{100}=1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com