Question

【題目】定義一個“希望結合”（）簡稱如下：為一個非空集合，它滿足條件“若，則”。試問：在集合中，一共有多少個“希望子集合”？請說明理由。

Answer 1

【答案】

【解析】

下面用“”表示與的兩倍關系.注意到

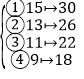
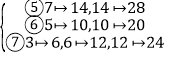
顯然，是否在中不影響成為希望子集（因為這些數不能被整除，且每個數的兩倍均大于），所以，這個數的歸屬方案有種.

在①中，與不能同時取，故有種方案.

同理，在②、③、④中，也各有種方案.

下面采用遞推算法.

在⑤中，若取，則不能取，此時，可取亦可不取，有兩種方案：若不取，則由①知，關于和，共有種方案（和的情況與①相同）.因此，在⑤中共有種方案.

同理，在⑥中共有種方案.

在⑦中，若取，則不能取，由①知關于和，有種方案；若不取，則由⑤知，關于有種方案.因此，在⑦中共有種方案.

在⑧中，若取，則不能取，由⑤知關于，有種方案；若不取，則由⑦知關于，有種方案.因此，在⑧中共有種方案.

再考慮到除去空集（即都不取），因此所求的的希望子集的個數為.