
【題目】已知函數(shù)![]() ,其中
,其中![]() .
.
(1)當(dāng)![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)記![]() 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為![]() ,若不等式
,若不等式![]() 在區(qū)間
在區(qū)間![]() 上恒成立,求
上恒成立,求![]() 的取值范圍;
的取值范圍;
(3)設(shè)函數(shù)![]() ,
,![]() 是函數(shù)
是函數(shù)![]() 的導(dǎo)函數(shù),若
的導(dǎo)函數(shù),若![]() 存在兩個極值點
存在兩個極值點![]() ,
,![]() ,且滿足
,且滿足![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(Ⅰ)當(dāng)![]() 時,
時,![]() ,
,![]() (1)
(1)![]() .
.![]() ,可得
,可得![]() (1)
(1)![]() .利用點斜式即可得出切線方程.
.利用點斜式即可得出切線方程.
(Ⅱ)![]() ,
,![]() .不等式
.不等式![]() ,化為:
,化為:![]() .令
.令![]() 在
在![]() 上恒成立,
上恒成立,![]() (1)
(1)![]() .可得
.可得![]() 在
在![]() 上恒成立,化為:
上恒成立,化為:![]() 即可得出.
即可得出.
(Ⅲ)根據(jù)![]() 可得
可得![]() 和
和![]() 關(guān)于x的函數(shù)表達式,根據(jù)
關(guān)于x的函數(shù)表達式,根據(jù)![]() 存在兩個極值點
存在兩個極值點![]() ,
,![]() ,可得
,可得![]() =0在
=0在![]() 上有兩個不等實數(shù)根
上有兩個不等實數(shù)根![]() ,
,![]() .因此
.因此![]() ,得出a的取值范圍.并根據(jù)
,得出a的取值范圍.并根據(jù)![]() ,
,![]() 滿足
滿足![]() ,代入簡化,利用導(dǎo)數(shù)研究其單調(diào)性即可得出結(jié)果.
,代入簡化,利用導(dǎo)數(shù)研究其單調(diào)性即可得出結(jié)果.
解:(Ⅰ)當(dāng)![]() 時,
時,![]() ,
,![]() (1)
(1)![]() .
.
![]() ,
,![]() (1)
(1)![]() .
.
![]() 曲線
曲線![]() 在點(1,
在點(1,![]() )處的切線方程為:
)處的切線方程為:![]() ,化為:
,化為:![]() .
.
(Ⅱ)![]() ,
,![]() .
.
不等式![]() ,即
,即![]() ,化為:
,化為:![]() .
.
令![]() 在
在![]() 上恒成立,
上恒成立,![]() (1)
(1)![]() .
.
![]() 在
在![]() 上恒成立,化為:
上恒成立,化為:![]() .
.
![]() 的取值范圍是
的取值范圍是![]() .
.
(Ⅲ)設(shè)函數(shù)![]() ,
,
![]() ,
,![]() .
.
![]() 存在兩個極值點
存在兩個極值點![]() ,
,![]() ,
,
![]() 在
在![]() 上有兩個不等實數(shù)根
上有兩個不等實數(shù)根![]() ,
,![]() .
.
因此![]() ,且
,且![]() ,
,![]() .
.
解得![]() .
.
![]() ,
,![]() ,滿足
,滿足![]() ,
,
![]()
![]() .
.
化為:![]() .
.
![]()
![]() ,
,![]() .
.
化為:![]() ,
,
令![]() (a)
(a)![]() ,
,![]() ,
,![]() (1)
(1)![]() .
.
![]() ,
,
![]() (a)在
(a)在![]() 上單調(diào)遞增,
上單調(diào)遞增,
![]()
![]() .
.
![]() 實數(shù)
實數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.


 世紀(jì)百通期末金卷系列答案
世紀(jì)百通期末金卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=ex(ax+b)-x2-4x,曲線y=f(x)在點(0,f(0))處的切線方程為y=4x+4.
(Ⅰ)求a,b的值;
(Ⅱ)討論f(x)的單調(diào)性.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】請你設(shè)計一個包裝盒,如圖所示,![]() 是邊長為
是邊長為![]() 的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得
的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得![]() 四個點重合于圖中的點
四個點重合于圖中的點![]() ,正好形成一個正四棱柱形狀的包裝盒,
,正好形成一個正四棱柱形狀的包裝盒,![]() 在
在![]() 上,是被切去的一個等腰直角三角形斜邊的兩個端點,設(shè)
上,是被切去的一個等腰直角三角形斜邊的兩個端點,設(shè)![]() (
(![]() ).
).

(1)某廣告商要求包裝盒的側(cè)面積![]()
![]() 最大,試問
最大,試問![]() 應(yīng)取何值?
應(yīng)取何值?
(2)某廠商要求包裝盒的容積![]() 最大,試問
最大,試問![]() 應(yīng)取何值?并求出此時包裝盒的高與底面邊長的比值.
應(yīng)取何值?并求出此時包裝盒的高與底面邊長的比值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】小趙和小王約定在早上![]() 至
至![]() 之間到某公交站搭乘公交車去上學(xué),已知在這段時間內(nèi),共有
之間到某公交站搭乘公交車去上學(xué),已知在這段時間內(nèi),共有![]() 班公交車到達該站,到站的時間分別為
班公交車到達該站,到站的時間分別為![]() ,
,![]() ,如果他們約定見車就搭乘,則小趙和小王恰好能搭乘同一班公交車去上學(xué)的概率為__________.
,如果他們約定見車就搭乘,則小趙和小王恰好能搭乘同一班公交車去上學(xué)的概率為__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某汽車公司對最近6個月內(nèi)的市場占有率進行了統(tǒng)計,結(jié)果如表;
月份代碼 | 1 | 2 | 3 | 4 | 5 | 6 |
市場占有率 | 11 | 13 | 16 | 15 | 20 | 21 |
(1)可用線性回歸模型擬合![]() 與
與![]() 之間的關(guān)系嗎?如果能,請求出
之間的關(guān)系嗎?如果能,請求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程,如果不能,請說明理由;
的線性回歸方程,如果不能,請說明理由;
(2)公司決定再采購![]() 兩款車擴大市場,
兩款車擴大市場, ![]() 兩款車各100輛的資料如表:
兩款車各100輛的資料如表:
車型 | 報廢年限(年) | 合計 | 成本 | |||
1 | 2 | 3 | 4 | |||
| 10 | 30 | 40 | 20 | 100 | 1000元/輛 |
| 15 | 40 | 35 | 10 | 100 | 800元/輛 |
平均每輛車每年可為公司帶來收入![]() 元,不考慮采購成本之外的其他成本,假設(shè)每輛車的使用壽命部是整數(shù)年,用每輛車使用壽命的頻率作為概率,以每輛車產(chǎn)生利潤的平均數(shù)作為決策依據(jù),應(yīng)選擇采購哪款車型?
元,不考慮采購成本之外的其他成本,假設(shè)每輛車的使用壽命部是整數(shù)年,用每輛車使用壽命的頻率作為概率,以每輛車產(chǎn)生利潤的平均數(shù)作為決策依據(jù),應(yīng)選擇采購哪款車型?
參考數(shù)據(jù): ![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:相關(guān)系數(shù)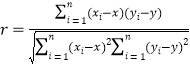 ;
;
回歸直線方程為![]() ,其中
,其中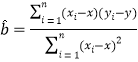 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】近年來,國資委.黨委高度重視扶貧開發(fā)工作,堅決貫徹落實中央扶貧工作重大決策部署,在各個貧困縣全力推進定點扶貧各項工作,取得了積極成效,某貧困縣為了響應(yīng)國家精準(zhǔn)扶貧的號召,特地承包了一塊土地,已知土地的使用面積以及相應(yīng)的管理時間的關(guān)系如下表所示:
土地使用面積 | 1 | 2 | 3 | 4 | 5 |
管理時間 | 8 | 10 | 13 | 25 | 24 |
并調(diào)查了某村300名村民參與管理的意愿,得到的部分?jǐn)?shù)據(jù)如下表所示:
愿意參與管理 | 不愿意參與管理 | |
男性村民 | 150 | 50 |
女性村民 | 50 |
(1)求出相關(guān)系數(shù)![]() 的大小,并判斷管理時間
的大小,并判斷管理時間![]() 與土地使用面積
與土地使用面積![]() 是否線性相關(guān)?
是否線性相關(guān)?
(2)是否有99.9%的把握認為村民的性別與參與管理的意愿具有相關(guān)性?
(3)若以該村的村民的性別與參與管理意愿的情況估計貧困縣的情況,則從該貧困縣中任取3人,記取到不愿意參與管理的男性村民的人數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學(xué)期望。
的分布列及數(shù)學(xué)期望。
參考公式:
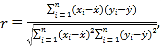
![]()
其中![]() 。臨界值表:
。臨界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
參考數(shù)據(jù):![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐PABCD中,底面ABCD是矩形,點E在棱PC上![]() 異于點P,
異于點P,![]() ,平面ABE與棱PD交于點F
,平面ABE與棱PD交于點F

![]() 求證:
求證:![]() ;
;
![]() 若
若![]() ,求證:平面
,求證:平面![]() 平面ABCD.
平面ABCD.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com