Question

4．過拋物線y²=2px（p＞0）的焦點F的直線l與拋物線在第一象限的交點為A，與拋物線的準線的交點為B，點A在拋物線的準線上的射影為C，若$\overrightarrow{AF}=\overrightarrow{FB}$，$\overrightarrow{BA}•\overrightarrow{BC}=12$，則拋物線的方程為y²=2x．

Answer 1

分析 判斷F為A，B的中點，設出B，求出A，C坐標，利用向量的數量積求解即可．

解答 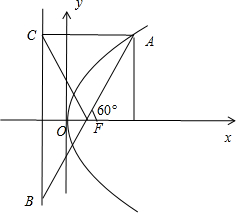解：過拋物線y²=2px（p＞0）的焦點F的直線l與拋物線
在第一象限的交點為A，
與拋物線的準線的交點為B，點A在拋物線的準線上的射影為C，
若$\overrightarrow{AF}=\overrightarrow{FB}$，可知F（$\frac{p}{2}，0$）是AB的中點，設B（$-\frac{p}{2}$，-n）n＞0，則A（$\frac{3P}{2}，n$），
C（-$\frac{p}{2}$，n），$\overrightarrow{BA}$=（2p，2n，$\overrightarrow{BC}$=（0，2n），
$\overrightarrow{BA}•\overrightarrow{BC}=12$，可得：4n²=12，解得n=$\sqrt{3}$，|BC|=2$\sqrt{3}$
|AF|=|AC|=2p=$\frac{\frac{1}{2}|BC|}{sin60°}$=2．
所求拋物線方程為：y²=2x．
故答案為：y²=2x．

點評 本題考查拋物線的可的性質的應用，直線與拋物線的位置關系的應用，考查計算能力．