
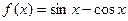 ,
,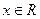 .(1)求函數(shù)
.(1)求函數(shù)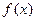 在
在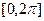 內(nèi)的單調(diào)遞增區(qū)間;
內(nèi)的單調(diào)遞增區(qū)間;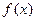 在
在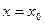 處取到最大值,求
處取到最大值,求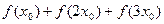 的值;
的值;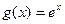 (
(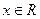 ),求證:方程
),求證:方程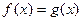 在
在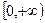 內(nèi)沒有實數(shù)解.(參考數(shù)據(jù):
內(nèi)沒有實數(shù)解.(參考數(shù)據(jù): ,
,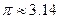 )
)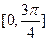 和
和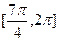 (Ⅱ)
(Ⅱ) 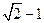 (Ⅲ)見解析
(Ⅲ)見解析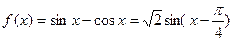 ,令
,令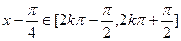 (
(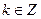 )
)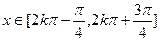 ,----------------2分
,----------------2分 ,則
,則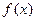 在
在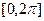 內(nèi)的單調(diào)遞增區(qū)間為
內(nèi)的單調(diào)遞增區(qū)間為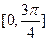 和
和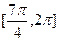 ;
;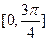
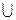
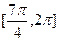 的形式扣1分)
的形式扣1分)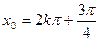 (
(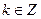 ),-------6分由周期性,
),-------6分由周期性,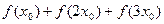
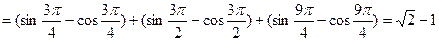 ;-----------------8分
;-----------------8分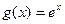 (
(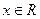 )為單調(diào)增函數(shù),
)為單調(diào)增函數(shù),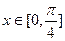 時,
時,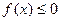 ,
,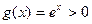 ,此時有
,此時有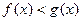 ;-------------10分
;-------------10分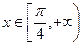 時,由于
時,由于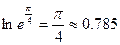 ,而
,而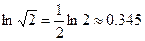 ,
,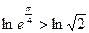 ,即
,即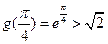 ,
,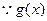 為增函數(shù),
為增函數(shù),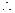 當
當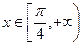 時,
時,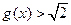 ------12分
------12分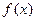 的最大值為
的最大值為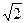 ,即
,即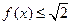 ,則當
,則當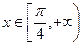 時,恒有
時,恒有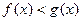 ,
,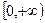 恒有
恒有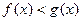 ,即方程
,即方程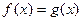 在
在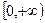 內(nèi)沒有實數(shù)解.
內(nèi)沒有實數(shù)解.

科目:高中數(shù)學 來源:不詳 題型:解答題
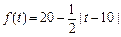 (元).
(元).查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
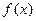 滿足
滿足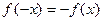 ,函數(shù)
,函數(shù)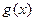 滿足
滿足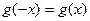 ,且對任意
,且對任意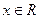 有
有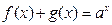 (
(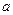 >0,且
>0,且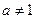 )
)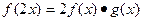 ;
;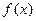 的反函數(shù)為
的反函數(shù)為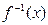 ,當
,當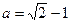 時,試比較
時,試比較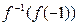 與
與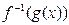 的大小
的大小查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
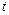 元(其中
元(其中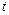 為常數(shù),且
為常數(shù),且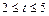 ),設(shè)該工廠每件玩具的出廠價為
),設(shè)該工廠每件玩具的出廠價為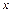 元(
元(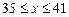 ),根據(jù)市場調(diào)查,日銷售量與
),根據(jù)市場調(diào)查,日銷售量與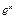 (
(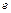 為自然對數(shù)的底數(shù))成反比例,當每件玩具的出廠價為40元時,日銷售量為10件.
為自然對數(shù)的底數(shù))成反比例,當每件玩具的出廠價為40元時,日銷售量為10件.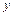 (元)與每件玩具的出廠價
(元)與每件玩具的出廠價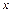 元的函數(shù)關(guān)系式;
元的函數(shù)關(guān)系式;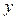 最大,并求
最大,并求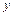 的最大值.
的最大值.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
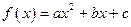 .
.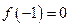 ,試判斷函數(shù)
,試判斷函數(shù)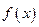 零點個數(shù);
零點個數(shù);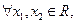 且
且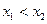 ,
,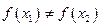 ,試證明
,試證明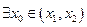 ,使
,使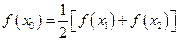 成立。
成立。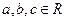 ,使
,使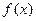 同時滿足以下條件①對
同時滿足以下條件①對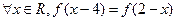 ,且
,且 ;②對
;②對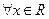 ,都有
,都有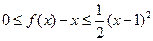 。若存在,求出
。若存在,求出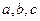 的值,若不存在,請說明理由。
的值,若不存在,請說明理由。查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
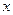 艘產(chǎn)值函數(shù)為
艘產(chǎn)值函數(shù)為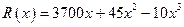 (單位:萬元),成本函數(shù)
(單位:萬元),成本函數(shù)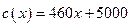 (單位:萬元),又在經(jīng)濟學中,函數(shù)
(單位:萬元),又在經(jīng)濟學中,函數(shù)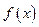 的邊際函數(shù)
的邊際函數(shù)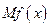 定義為
定義為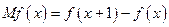
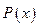 及邊際利潤函數(shù)
及邊際利潤函數(shù)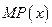 (利潤=產(chǎn)值—成本)
(利潤=產(chǎn)值—成本)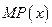
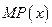 的單調(diào)遞減區(qū)間
的單調(diào)遞減區(qū)間查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
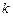 和
和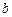 ,使得函數(shù)
,使得函數(shù)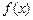 和
和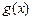 對其定義域上的任意實數(shù)
對其定義域上的任意實數(shù)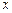 分別滿足:
分別滿足: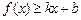 和
和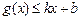 ,則稱直線
,則稱直線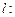
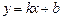 為
為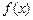 和
和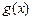 的“隔離直線”.已知
的“隔離直線”.已知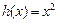 ,
,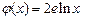 (其中
(其中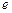 為自然對數(shù)的底數(shù)),根據(jù)你的數(shù)學知識,推斷
為自然對數(shù)的底數(shù)),根據(jù)你的數(shù)學知識,推斷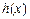 與
與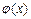 間的隔離直線方程為 .
間的隔離直線方程為 .查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com